Práctico 5: Asociación entre categóricas

Sesión del martes, 15 de octubre de 2024

Objetivo de la práctica

El objetivo de esta guía práctica es introducir herramientas estadísticas para el análisis de relación entre variables categóricas (nominales).

En detalle, aprenderemos a:

1. Aplicar coeficientes de correlación entre variables categóricas (nominales-ordinales)
2. Generar y analizar tablas de contingencia (o cruzadas)
3. Estimar e interpretar la prueba de Chi-cuadrado (\(X^2\))
4. Interpretar medidas de magnitud para pruebas con variables categóricas
5. Realizar pruebas de hipótesis para proporciones

En esta guía utilizaremos un ejemplo que desarrollaremos progresivamente para exponer los contenidos. Al final de esta guía se proporciona un ejercicio autónomo que deberá resolver de manera individual o grupal tomando como referencia el ejemplo aquí expuesto.

1. Pregunta de investigación

La violencia es un fenómeno con el que se debe coexistir, estableciendo límites para su uso. Las movilizaciones de 2019 en Chile representan un ejemplo de un evento que aumentó la justificación de la violencia como protesta y redujo la justificación de la violencia policial, lo que plantea preguntas sobre quiénes y por qué justifican la violencia.

El estudio de las justificaciones de la violencia distingue si esta se ejerce por el cambio social o por el control social. La violencia por el cambio social refiere a acciones que tengan por objetivo generar cambios en las estructuras jerarquicas de la sociedad, en tanto, la violencia por el control social refiere a aquellas acciones que tienen por objetivo mantener estas estructuras.

En la literatura, uno de los principales hallazgos es que personas que pertenecen a grupos desavantejados (ej. nivel socioeconómico) suelen justificar más la violencia por el cambio social y menos por el control social.

Considerando estos antecedentes, plantearemos dos preguntas de investigación:

Pregunta 1: ¿En qué medida se relacionan los ingresos con la justificación de la violencia por el cambio social en Chile al año 2019?

H1: A mayores ingresos, menor es la justificación de la violencia por el cambio social

Pregunta 2: ¿En qué medida se relacionan el el nivel educacional con la justificación de la violencia por el control social en Chile al año 2019?

H2: A mayor nivel educacional, mayor es la justificación de la violencia por el control social

Recursos de la práctica

En esta práctica trabajaremos con un subconjunto de datos previamente procesados de la Encuesta Social Longitudinal de Chile (ELSOC) para Chile del año 2019. Para este ejercicio, obtendremos directamente esta base desde internet. No obstante, también es posible acceder a la misma información a través del siguiente enlace: ELSOC 2019. Desde allí, podrás descargar el archivo que contiene el subconjunto procesado de la base de datos ELSOC 2019.

2. Datos y librerías

Comencemos por preparar nuestros datos. Iniciamos cargando las librerías necesarias.

pacman::p_load(
    tidyverse, # Manipulacion datos
    sjPlot, # Graficos y tablas
    sjmisc, # Descriptivos
    kableExtra, # Tablas
    psych, # Estadísticos
    broom
) # Varios

options(scipen = 999) # para desactivar notacion cientifica
rm(list = ls()) # para limpiar el entorno de trabajo

Cargamos los datos directamente desde internet.

# Cargar bbdd desde internet
load(url("https://github.com/cursos-metodos-facso/datos-ejemplos/raw/refs/heads/main/elsoc2019_jv.RData"))

A continuación, exploramos el subset de datos elsoc.

names(elsoc) # Nombre de columnas

 [1] "jv_control"                "jv_cambio"                
 [3] "salario_perc_ceo"          "salario_perc_obrero"      
 [5] "salario_just_ceo"          "salario_just_obrero"      
 [7] "ingreso_justo"             "ingreso"                  
 [9] "ingreso_tramos"            "educ"                     
[11] "ingreso_satisfact"         "sexo"                     
[13] "indigena"                  "sdo_soc_ideal"            
[15] "sdo_grupos_inferiores"     "sdo_oportunidades_iguales"
[17] "sdo_condiciones_iguales"   "rwa_gobierno_firme"       
[19] "rwa_mandatario_fuerte"     "rwa_valores_ninos"        
[21] "rwa_obediencia_discplina"  "trato_carab"              
[23] "edad"                      "pos_pol"                  
[25] "frec_marcha"               "conf_carab"               
[27] "sj_gerente"                "sj_gerente_rec"           
[29] "jv_cambio_rec"             "jv_control_rec"           
[31] "ingreso_rec"               "educ_rec"                 

dim(elsoc) # Dimensiones

[1] 3417   32

Contamos con 32 variables (columnas) y 3417 observaciones (filas).

Ahora, realizaremos un pequeño procesamiento de nuestros datos con dplyr, todo de una vez mediante el uso de pipes %>%. Para recordar los pasos para el procesamiento de datos, revisar la guía práctica del curso de estadística descriptiva.

proc_elsoc <- elsoc %>% # seleccionamos
    dplyr::select(
        ingreso,
        ingreso_rec,
        educ,
        educ_rec,
        starts_with("jv")
    )

Ahora, exploremos estadísticos descriptivos de nuestra base procesada proc_elsoc

proc_elsoc %>%
    select(ingreso, ingreso_rec, educ, educ_rec, jv_cambio, jv_cambio_rec, jv_control, jv_control_rec) %>%
    sjmisc::descr(show = c("label", "range", "mean", "sd", "NA.prc", "n")) %>%
    kable(., "markdown")

	var	label	n	NA.prc	mean	sd	range
3	ingreso	Ingresos del entrevistado	2018	40.9423471	537927.1560951	587217.4858725	15000000 (0-15000000)
4	ingreso_rec	Ingresos mayores a 800.000 (binario)	2018	40.9423471	0.1367691	0.3436886	1 (0-1)
1	educ	Nivel educacional del entrevistado	3413	0.1170618	5.2510987	2.2385444	9 (1-10)
2	educ_rec	Educación universitaria o más (binario)	3413	0.1170618	0.1259889	0.3318854	1 (0-1)
5	jv_cambio	Justificación de la violencia por el cambio social	3405	0.3511853	1.4763583	0.9551252	4 (1-5)
6	jv_cambio_rec	Justificación de la violencia por el cambio social (binario)	3405	0.3511853	0.2499266	0.4330339	1 (0-1)
7	jv_control	Justificación de la violencia por el control social	3407	0.2926544	1.4029938	0.8712963	4 (1-5)
8	jv_control_rec	Justificación de la violencia por el control social (binario)	3407	0.2926544	0.2180804	0.4130029	1 (0-1)

3. Análisis

En ELSOC 2019 la justificación de la violencia se mide con una escala que incluye distintas situaciones de violencia. Nosotros tomaremos dos items:

Justificación de la violencia: F05 ¿En qué medida cree usted que se justifican o no se justifican las siguientes situaciones?

Ítem	Categorías de respuesta
F05_03 Que Carabineros use la fuerza para reprimir una manifestación pacífica	Nunca se justifica (1); Pocas veces se justifica (2); Algunas veces de justifica (3); Muchas veces se justifica (4); Siempre se justifica (5)
F05_07 Que estudiantes tiren piedras a Carabineros en una marcha por la educación del país	Nunca se justifica (1); Pocas veces se justifica (2); Algunas veces de justifica (3); Muchas veces se justifica (4); Siempre se justifica (5)

Veamos sus frecuencias:

plot1 <- sjPlot::plot_frq(proc_elsoc$jv_cambio) + coord_flip() + theme_minimal()
plot2 <- sjPlot::plot_frq(proc_elsoc$jv_control) + coord_flip() + theme_minimal()

plot1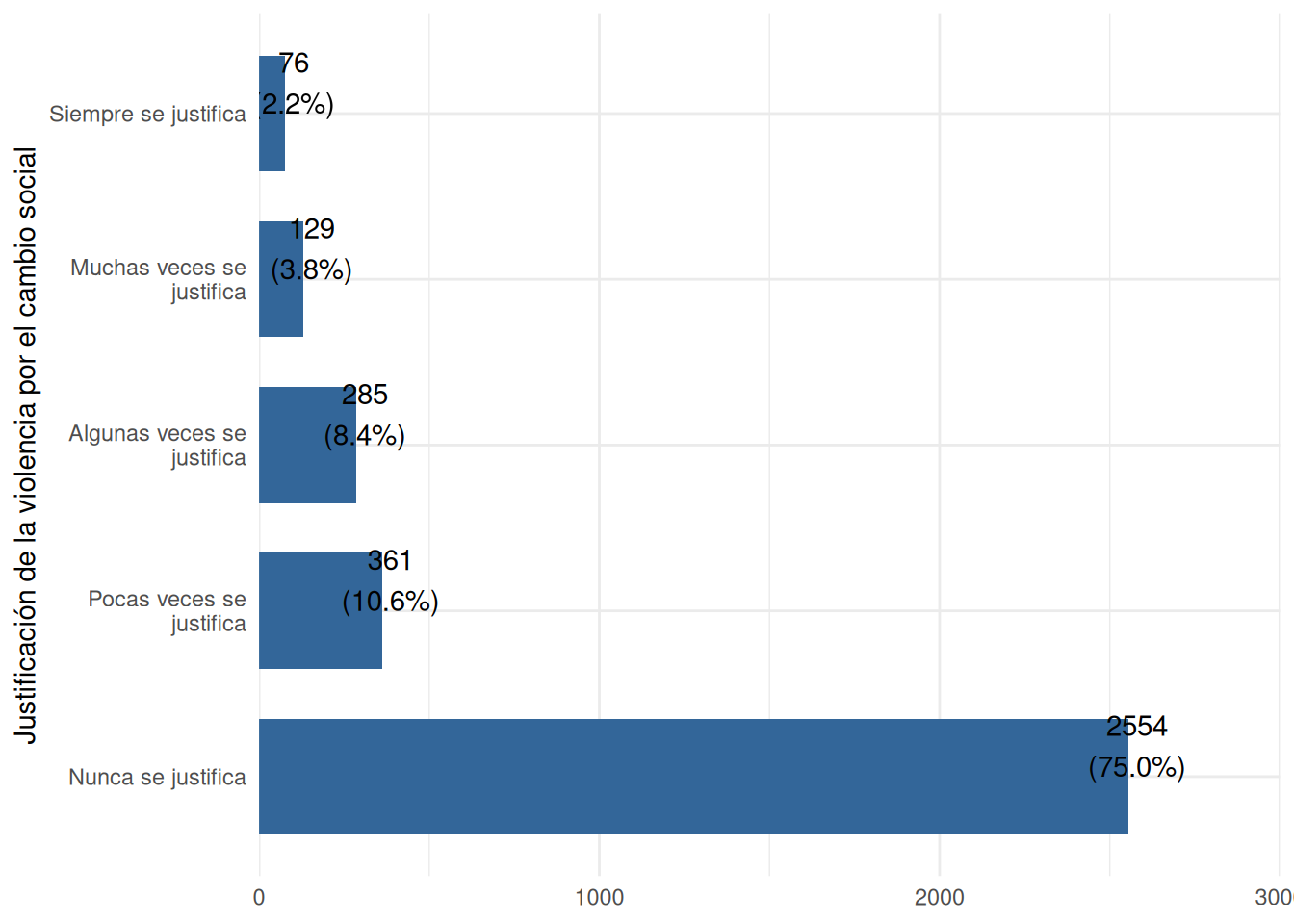

plot2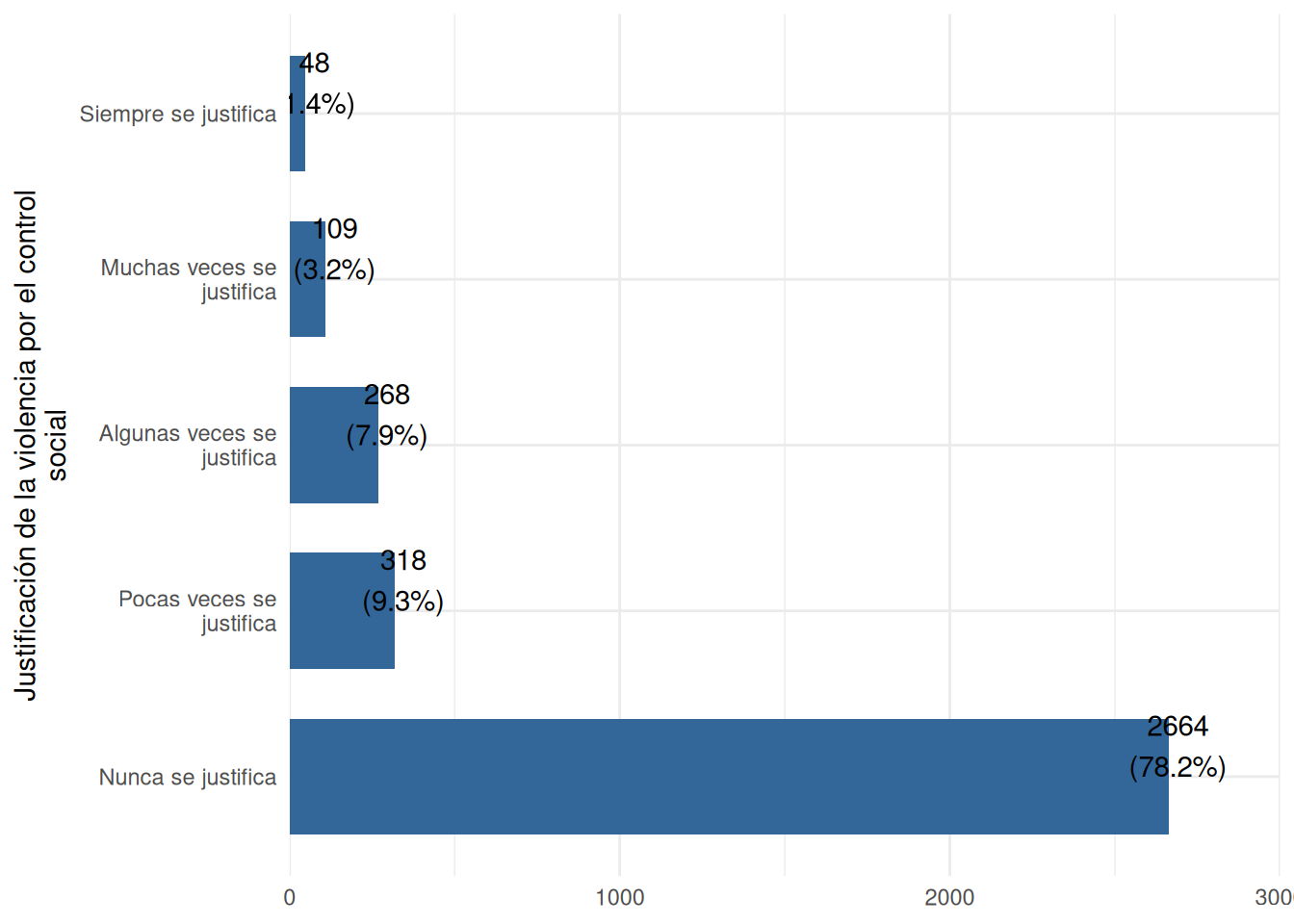

Originalmente, esta variable es ordinal, sin embargo, para efectos del ejemplo de este práctico, trabajaremos con la variable recodificada de la siguiente manera:

• Justifica (1) = Pocas veces se justifica (2); Algunas veces de justifica (3); Muchas veces se justifica (4); Siempre se justifica (5)
• No justifica (0) = Nunca se justifica (1)

3.1 Correlación para variables nominales

3.1.1 Correlación punto biserial

La correlación punto biserial es una extensión del coeficiente de correlación de Pearson y se utiliza cuando una de las variables de estudio tienen un nivel de medición intervalar y la otra un nivel de medición nominal.

• El nombre de punto biserial es una forma de diferenciarla de la correlación de Pearson
• Esta diferenciación es importante ya que nos prevee de que hay que tener consideraciones con su interpretación, particularmente en lo que refiere al sentido
• En lo que respecta a la magnitud/tamaño y la inferencia, sigue la misma lógica que hemos visto con la correlación de Pearson

Para calcular este coeficiente en R utilizamos una función ya conocida: cor.test(). Probemoslo con las variables jv_cambio_rec e ingreso.

Primero, veamos la frecuencia de jv_cambio_rec e ingreso.

sjmisc::frq(proc_elsoc$jv_cambio_rec)
## Justificación de la violencia por el cambio social (binario) (x) <numeric> 
## # total N=3417 valid N=3405 mean=0.25 sd=0.43
## 
## Value |        Label |    N | Raw % | Valid % | Cum. %
## ------------------------------------------------------
##     0 | No justifica | 2554 | 74.74 |   75.01 |  75.01
##     1 |    Justifica |  851 | 24.90 |   24.99 | 100.00
##  <NA> |         <NA> |   12 |  0.35 |    <NA> |   <NA>

mean(proc_elsoc$ingreso, na.rm = TRUE)
## [1] 537927.2

Obtengamos la correlación punto biserial entre el ingreso y la justificación de la violencia por el cambio social.

cor.test(proc_elsoc$jv_cambio_rec, proc_elsoc$ingreso)

    Pearson's product-moment correlation

data:  proc_elsoc$jv_cambio_rec and proc_elsoc$ingreso
t = -0.51503, df = 2010, p-value = 0.6066
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.05515929  0.03222920
sample estimates:
        cor 
-0.01148698 

Vemos que la correlación entre el ingreso (ingreso) y la justificación de la violencia por el cambio social (jv_cambio_rec) es negativa, muy pequeña y no es estadísticamente significativa (\(r\) = -0.01; p > 0.05).

3.1.2 Correlación tetracorica

La correlación tetracórica también es una extensión del coeficiente de correlación de Pearson, con la diferencia de que se usa cuando ambas variables de estudio son nominales dicotomicas (2 valores).

• Se calcula en base a la frecuencias de cada combinación de valores (00,01,10,11).
• Supone que ambas variables son continuas y normalmente distribuidas antes de la categorización

Veamos como vería una correlación tetracórica entre nuestras variables de estudio. En este caso, vamos a usar jv_cambio_rec que ya es dicotomica (1 = Justifica, 0 = No justifica) y una versión recodificada del ingreso ingreso_rec, la cual identifica aquellos entrevistados que tienen un ingreso mayor o menor a 800.000 pesos (1 = Mayor a 800k, 0 = Menor a 800k)

Primero, veamos las frecuencias entre jv_cambio_rec e ingreso_rec.

sjmisc::frq(proc_elsoc$jv_cambio_rec)
## Justificación de la violencia por el cambio social (binario) (x) <numeric> 
## # total N=3417 valid N=3405 mean=0.25 sd=0.43
## 
## Value |        Label |    N | Raw % | Valid % | Cum. %
## ------------------------------------------------------
##     0 | No justifica | 2554 | 74.74 |   75.01 |  75.01
##     1 |    Justifica |  851 | 24.90 |   24.99 | 100.00
##  <NA> |         <NA> |   12 |  0.35 |    <NA> |   <NA>

sjmisc::frq(proc_elsoc$ingreso_rec)
## Ingresos mayores a 800.000 (binario) (x) <numeric> 
## # total N=3417 valid N=2018 mean=0.14 sd=0.34
## 
## Value |        Label |    N | Raw % | Valid % | Cum. %
## ------------------------------------------------------
##     0 | Menor a 800k | 1742 | 50.98 |   86.32 |  86.32
##     1 | Mayor a 800k |  276 |  8.08 |   13.68 | 100.00
##  <NA> |         <NA> | 1399 | 40.94 |    <NA> |   <NA>

Obtengamos la correlación tetracórica entre jv_cambio_rec e ingreso_rec.

matriz <- proc_elsoc %>%
    dplyr::select(jv_cambio_rec, ingreso_rec) # creamos matriz con var de interes

psych::tetrachoric(matriz, na.rm = T)

Call: psych::tetrachoric(x = matriz, na.rm = T)
tetrachoric correlation 
              jv_c_ ingr_
jv_cambio_rec 1.00       
ingreso_rec   0.02  1.00 

 with tau of 
jv_cambio_rec   ingreso_rec 
         0.67          1.09 

Vemos que la correlación entre los ingresos recodificados (ingreso_rec) y la justificación de la violencia por el cambio social (jv_cambio_rec) es positiva y muy pequeña (\(r\) = 0.02).

3.2 Tablas de contingencia

Las tablas de contingencia son herramientas estadísticas utilizadas para resumir y analizar la relación entre dos o más variables categóricas. Estas tablas muestran la frecuencia de diferentes combinaciones de categorías de las variables, facilitando la visualización de patrones o asociaciones.

Dicho de otra manera, podemos saber cuántos casos de una determinada categoría de la variable \(Y\) ocurren conjuntamente con una determinada categoría de la variable \(X\).

Veamos una tabla con nuestro ejemplo usando el comando sjtab.

proc_elsoc %>%
    sjPlot::sjtab(ingreso_rec,
        jv_cambio_rec,
        show.row.prc = TRUE, # porcentaje fila
        show.col.prc = TRUE # porcentaje columna
    )

Ingresos mayores a 800.000 (binario)	Justificación de la violencia por el cambio social (binario)		Total
	No justifica	Justifica
Menor a 800k	1273 73.3 % 86.5 %	463 26.7 % 85.7 %	1736 100 % 86.3 %
Mayor a 800k	199 72.1 % 13.5 %	77 27.9 % 14.3 %	276 100 % 13.7 %
Total	1472 73.2 % 100 %	540 26.8 % 100 %	2012 100 % 100 %
χ2=0.126 · df=1 · &phi=0.010 · p=0.723

En esta tabla vemos que los porcentajes coloreados en azul corresponde a las filas y el verde el porcentaje que corresponde a las columnas. Utilizando esta información podemos decir, por ejemplo:

• El 72.1% de quienes ganan más de 800k no justifica la violencia por el cambio social

• El 13.5% de quienes no justifican la violencia por el cambio social ganan más de 800k

Ahora, ¿cómo sabemos si hay asociación? Repliquemos el ejemplo que vimos en clases, utilizando nuestras variables. Imaginemos que tenemos una base de datos con N = 100.

# Ejemplo de asociación perfecta
tab1 <- data.frame(
    "." = c("Menor a 800k", "Mayor a 800k", "Total"),
    `No justifica` = c(0, 50, 50),
    "Justifica" = c(50, 0, 50),
    Total = c(50, 50, 100)
)

# Ejemplo de no asociación
tab2 <- data.frame(
    "." = c("Menor a 800k", "Mayor a 800k", "Total"),
    `No justifica` = c(25, 25, 50),
    "Justifica" = c(25, 25, 50),
    Total = c(50, 50, 100)
)

Una distribución con evidencia “perfecta” para nuestra hipótesis alternativa se puede ver en la siguiente tabla:

tab1 %>%
    kable(format = "html", align = "r", col.names = c("Ingreso", "No justifica violencia", "Justifica violencia", "Total")) %>%
    kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"), full_width = T) %>%
    kableExtra::kable_styling(latex_options = "hold_position", position = "center")

Ingreso	No justifica violencia	Justifica violencia	Total
Menor a 800k	0	50	50
Mayor a 800k	50	0	50
Total	50	50	100

En contraste, una distribución que representaría un caso perfecto de no asociación, se puede ver en la siguiente tabla:

tab2 %>%
    kable(format = "html", align = "r", col.names = c("Ingreso", "No justifica violencia", "Justifica violencia", "Total")) %>%
    kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"), full_width = T) %>%
    kableExtra::kable_styling(latex_options = "hold_position", position = "center")

Ingreso	No justifica violencia	Justifica violencia	Total
Menor a 800k	25	25	50
Mayor a 800k	25	25	50
Total	50	50	100

3.3. Prueba de hipótesis con Chi cuadrado (\(X^2\))

Para determinar si existe una asociación significativa entre dos variables categóricas se utiliza la prueba de Chi-cudrado (\(X^2\)). Esta se basa en un test de diferencia, donde se compara nuestra tabla de contingencia y una tabla donde no existe asociación entre variables (\(H_0\)), que representa la hipótesis nula. La lógica detrás es que si nuestra tabla es significativamente distinta de una tabla sin asociación, entonces podemos rechazar la hipóteis nula.

Prueba de Chi-cuadrado

Contrastamos la hipótesis nula (o de trabajo) de que las variables son independientes entre ellas: \[ H_{0}: \pi_{fc} = \pi_{f}\pi_{c} \]

En relación a una hipótesis alternativa sobre que las variables están relacionadas: \[ H_{A}: \pi_{fc} \neq \pi_{f}\pi_{c} \]

En R, utilizamos la función chisq.test():

chi_results <- chisq.test(proc_elsoc$ingreso_rec, proc_elsoc$jv_cambio_rec)

chi_results

    Pearson's Chi-squared test with Yates' continuity correction

data:  proc_elsoc$ingreso_rec and proc_elsoc$jv_cambio_rec
X-squared = 0.1257, df = 1, p-value = 0.7229

Obtuvimos nuestro resultado, pero no es muy amigable a la vista. Generemos una tabla de calidad para que sea reportable.

stats.table <- tidy(chi_results)

stats.table %>%
    dplyr::mutate(
        statistic = round(statistic, 2),
        p_value = case_when(
            p.value < 0.05 & p.value > 0.01 ~ "< 0.05*",
            p.value < 0.01 & p.value > 0.001 ~ "< 0.01**",
            p.value < 0.001 ~ "< 0.001***",
            TRUE ~ ""
        )
    ) %>%
    dplyr::select(statistic, p_value, parameter, method) %>%
    kableExtra::kable(
        format = "html",
        col.names = c("X2", "p-value", "df", "Método"),
        booktabs = T,
        caption = "Prueba de Chi-cuadrado entre justificación de la violencia por cambio social e injusticia distributiva"
    ) %>%
    kableExtra::kable_styling(
        bootstrap_options = c("striped", "hover", "condensed", "responsive"),
        full_width = T,
        latex_options = "hold_position",
        position = "center"
    ) %>%
    column_spec(4, width = "8cm")

Tabla 1: Prueba de Chi-cuadrado entre justificación de la violencia por cambio social e injusticia distributiva

X2	p-value	df	Método
0.13		1	Pearson's Chi-squared test with Yates' continuity correction

A partir de estos resultados, podemos reportar lo siguiente:

A raíz de la prueba de \(X^2\), vemos que no existe evidencia para rechazar la hipótesis nula sobre no asociación. Por ende, la asociación entre los ingresos y la justificación de la violencia por el cambio social no es estadísticamente significativa (\(X^2\) = 0.126, p > 0.05)

3.4. Tamaño de efecto con Phi y V de Cramer

Estadístico Phi (Φ)

El estadístico Phi mide la asociación entre dos variables categóricas en una tabla de contingencia de 2x2. La fórmula es:

\[ \Phi = \sqrt{\frac{\chi^2}{n}} \]

donde:

• \(\chi^2\) es el valor del estadístico chi-cuadrado,
• \(n\) es el tamaño total de la muestra.

El valor de \(\Phi\) varía entre -1 y 1. Un valor de 0 indica ausencia de asociación, mientras que valores cercanos a -1 o 1 indican una asociación más fuerte.

V de Cramer

El V de Cramer es una extensión del estadístico Phi para tablas de contingencia mayores de 2x2. Su fórmula es:

\[ V = \sqrt{\frac{\chi^2}{n(k-1)}} \]

donde:

• \(\chi^2\) es el valor del chi-cuadrado,
• \(n\) es el tamaño de la muestra,
• \(k\) es el número de filas o columnas, el que sea menor.

Los valores de \(V\) también varían entre 0 y 1, donde 0 indica ausencia de asociación, y valores cercanos a 1 indican una asociación más fuerte.

En nuestro ejemplo, nuestra tabla de contingencia es de 2x2, por ende, debemos usar el estadístico Phi. En R lo podemos calcular directamente siguiendo la formula:

# Guardar el test de chi cuadrado
chi_result <- chisq.test(proc_elsoc$ingreso_rec, proc_elsoc$jv_cambio_rec)
n <- na.omit(proc_elsoc %>% select(ingreso_rec, jv_cambio_rec)) %>% nrow()

# Cálculo de Phi
phi <- sqrt(chi_result$statistic / n)
phi

  X-squared 
0.007904267 

Con un valor de 0.008, vemos que la magnitud de la asociación entre las variables es muy baja.

3.5 Test de proporciones

El test de proporciones es una prueba estadística que se utiliza para comparar las proporciones de éxito (o cualquier categoría de interés) entre dos o más grupos. Es especialmente útil cuando se trabaja con variables categóricas binarias (por ejemplo, sí/no, éxito/fallo) y queremos verificar si las proporciones de estas categorías son significativamente diferentes entre los grupos.

Este test evalúa la hipótesis nula de que las proporciones en diferentes grupos son iguales frente a la hipótesis alternativa de que al menos una de las proporciones es diferente.

En este caso, nos puede ser de utilidad si queremos conocer si la proporción de personas que justifican la violencia por el cambio social es estadísticamente diferente entre quienes tienen ingresos mayores a 800k y quienes tienen ingresos menores a 800k.

Esto se prueba en R de la siguiente manera:

# Veamos el conteo por categorías
table(proc_elsoc$ingreso_rec, proc_elsoc$jv_cambio_rec)

   
       0    1
  0 1273  463
  1  199   77

# Insertemos los datos a mano
prop.test(
    c(463, 77), # Conteo de exitos por grupo (Justifica x Menor a 800k y Justifica x Mayor a 800k)
    c((1273 + 463), (199 + 77)) # Suma por grupo (Menor a 800k y Mayor a 800k)
)

    2-sample test for equality of proportions with continuity correction

data:  c(463, 77) out of c((1273 + 463), (199 + 77))
X-squared = 0.1257, df = 1, p-value = 0.7229
alternative hypothesis: two.sided
95 percent confidence interval:
 -0.07123493  0.04667405
sample estimates:
   prop 1    prop 2 
0.2667051 0.2789855 

A raíz de la prueba de hipótesis de proporciones, podemos reportar lo siguiente:

Al 95% de confianza, no existe evidencia para rechazar la hipótesis nula de no diferencia en la proporción de personas que justifican la violencia por el cambio social entre ambas categorías de ingreso (p > 0.05). Es decir, no existen diferencias estadísticamente significativas en la proporción de personas que justifican la violencia por el cambio social entre quienes ganan más de 800k y menos de 800k.

4. Conclusiones

En el presente ejercicio indagamos en la relación entre los ingresos de las personas y las justificaciones de la violencia por el cambio social en Chile al año 2019. Considerando que las variables de estudio tenían un nivel de medición categórico nominal, utilizamos la técnica de Chi-cuadrado \(X^2\) para el contraste de hipótesis.

La hipótesis planteada inicialmente sugería que los ingresos podrían estar asociados con las actitudes hacia la justificación de la violencia como una forma de cambio social. Sin embargo, los resultados de la prueba \(X^2\), como se muestra en la Tabla 1, indican que no existe una asociación estadísticamente significativa entre estas variables (\(X^2\) = 0.126, p > 0.05).

Esto significa que, según los datos analizados, los ingresos no parecen ser un factor que influya en la justificación de la violencia para el cambio social. En otras palabras, las personas con diferentes niveles de ingresos no muestran diferenciasen sus actitudes hacia la justificación de la violencia. Por lo tanto, no podemos concluir que los ingresos estén relacionados con la justificación de la violencia en el contexto del cambio social en Chile en 2019.

Ejercicio autónomo

A partir de la base de datos de proc_elsoc responda la pregunta 2 planteada al inicio de este ejercicio. Es decir: ¿En qué medida se relacionan el nivel educacional y la justificación de la violencia por el control social en Chile al año 2019?

1. Estime la correlación adecuada para educ y jv_control_rec.

Para determinar cuál es la correlación adecuada entre educ y jv_control_rec tenemos que tener en consideración el nivel de medición de estas variables. Vemos que educ es continua y jv_control_rec es una variable categorica nominal binaria. Para estos casos, una buena alternativa es la correlación punto biserial. Estimemosla en R:

cor.test(proc_elsoc$educ, proc_elsoc$jv_control_rec)

    Pearson's product-moment correlation

data:  proc_elsoc$educ and proc_elsoc$jv_control_rec
t = -3.3769, df = 3401, p-value = 0.0007414
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.09123086 -0.02425427
sample estimates:
        cor 
-0.05780761 

Vemos que la correlación entre el nivel educacional (educ) y la justificación de la violencia por el control social (jv_control_rec) es negativa, muy pequeña y es estadísticamente significativa (\(r\) = -0.06; p < 0.05).

2. Presente en una tabla de contingencia entre las variables educ_rec y jv_control_rec.

Seguimos trabajando con jv_control_rec, pero ahora con educ_rec que corresponde al nivel educacional recodificado en dos categorías: 1 = Universitario o más y 0 = No universitario. Una tabla de contingencia la podemos realizar con la función sjtab() del paquete sjPlot.

sjPlot::sjtab(proc_elsoc, educ_rec, jv_control_rec, show.row.prc = TRUE, show.col.prc = TRUE)

Educación universitaria o más (binario)	Justificación de la violencia por el control social (binario)		Total
	No justifica	Justifica
No universitaria	2315 77.8 % 87 %	661 22.2 % 89.2 %	2976 100 % 87.5 %
Universitaria o más	347 81.3 % 13 %	80 18.7 % 10.8 %	427 100 % 12.5 %
Total	2662 78.2 % 100 %	741 21.8 % 100 %	3403 100 % 100 %
χ2=2.448 · df=1 · &phi=0.028 · p=0.118

3. Calcule el estadístico de Chi cuadrado (\(X^2\)) entre las variables educ_rec y jv_control_rec.

El Chi cuadrado (\(X^2\)) entre las variables educ_rec y jv_control_rec los podemos obtener a partir de la función chisq.test():

chisq.test(proc_elsoc$educ_rec, proc_elsoc$jv_control_rec)

    Pearson's Chi-squared test with Yates' continuity correction

data:  proc_elsoc$educ_rec and proc_elsoc$jv_control_rec
X-squared = 2.4482, df = 1, p-value = 0.1177

A partir de estos resultados, podemos reportar lo siguiente:

A raíz de la prueba de \(X^2\), vemos que no existe evidencia para rechazar la hipótesis nula sobre no asociación. Por ende, la asociación entre el nivel educacional y la justificación de la violencia por el control social no es estadísticamente significativa (\(X^2\) = 2.448, p > 0.05)

4. Interprete los resultados obtenidos. Responda la pregunta de investigación a raíz de los calculos desarrollados.

En el presente ejercicio indagamos en la relación entre el nivel educacional de las personas y las justificaciones de la violencia por el control social en Chile al año 2019. Considerando que las variables de estudio tenían un nivel de medición categórico nominal, utilizamos la técnica de Chi-cuadrado \(X^2\) para el contraste de hipótesis.

La hipótesis planteada inicialmente sugería que el nivel educacional podría estar asociado con las actitudes hacia la justificación de la violencia como una forma de control social. Sin embargo, los resultados de la prueba \(X^2\), indican que no existe una asociación estadísticamente significativa entre estas variables (\(X^2\) = 2.448, p > 0.05).

Esto significa que, según los datos analizados, el nivel educacional no parecen ser un factor que influya en la justificación de la violencia para el control social, por lo tanto, no podemos concluir que el nivel educacional estén relacionados con la justificación de la violencia en el contexto del cambio social en Chile en 2019.