Práctico 2: Intentando rechazar

Sesión del martes, 3 de septiembre de 2024

Objetivo de la práctica

El objetivo de esta guía práctica es realizar una serie de ejercicios de inferencia estadística, tomando como base todos los contenidos de la Unidad 1. En particular, se abordan pruebas de hipótesis para diferencias de medias y direccionales utilizando la prueba t

La guía tiene 3 ejercicios. El primero de ellos es un ejemplo, y los ejercicios 2 y 3 se desarrollan de manera autónoma en la sala (también puede ser en grupo).

Recursos de la práctica

En esta práctica trabajaremos con un subconjunto de datos previamente procesados de la Encuesta de Caracterización Socioeconómica (CASEN) del año 2022, elaborada por el Ministerio de Desarrollo Social y Familia. Para este ejercicio, obtendremos directamente esta base desde internet. No obstante, también tienes la opción de acceder a la misma información a través del siguiente enlace: CASEN 20222. Desde allí, podrás descargar el archivo que contiene el subconjunto procesado de la base de datos CASEN 2022.

Cinco pasos para la inferencia estadística

En inferencia, las pruebas de hipótesis nos ayudan a determinar si el resultado que obtenemos en nuestra muestra es un efecto real/extensible a la población o un error. Aquí recomendamos una lista de cinco pasos lógicos para enfrentarnos a la inferencia estadística:

Paso	Detalle
1	Formula \(H_0\) y \(H_A\) y estipula la dirección de la prueba
2	Calcula el error estándar (SE) y el valor estimado de la prueba (ej: Z o t)
3	Especifica la probabilidad de error \(\alpha\) y el valor crítico de la prueba
4	Contrasta el valor estimado con el valor crítico
5	Intrepreta los resultados

Además de estos 5 pasos también existe la posibilidad de calcular un intervalo de confianza, que acompañe la precisión de nuestra estimación.

Preparación datos

Comencemos por preparar nuestros datos. Iniciamos cargando las librerías necesarias.

pacman::p_load(dplyr, # Manipulacion datos
               gginference, # Visualizacion 
               rempsyc, # Reporte
               kableExtra, # Tablas
               broom) # Varios

options(scipen = 999) # para desactivar notacion cientifica
rm(list = ls()) # para limpiar el entorno de trabajo

Tip

Los # en el código

En este código y siguientes aparecen varios #, que son una función de comentarios en R. No son necesarios para que el código funcione, pero son útiles en este caso para poder explicar que función cumple cada sección del código. Todo lo que aparece a la derecha de un # no es leído por el programa.

Cargamos los datos directamente desde internet.

load(url("https://github.com/cursos-metodos-facso/datos-ejemplos/raw/main/proc_casen.RData")) #Cargar base de datos

A continuación, exploramos la base de datos proc_casen.

names(proc_casen) # Nombre de columnas

 [1] "id_vivienda"      "folio"            "id_persona"       "hogar"           
 [5] "nucleo"           "varunit"          "varstrat"         "expr"            
 [9] "edad"             "sexo"             "educ"             "activ"           
[13] "y1"               "ytrabajocor"      "pobreza_multi_5d" "o15"             
[17] "qaut"             "fdt"              "ocupado"          "desocupado"      
[21] "inact"            "hijo"             "n_educ"           "universitaria"   
[25] "tipo_ocup"        "ss_salud"         "ayuda_moverse"    "ayuda_thogar"    
[29] "disc_fisica"     

dim(proc_casen) # Dimensiones

[1] 202111     29

Contamos con 24 variables (columnas) y 202.111 observaciones (filas).

Recordemos…

En estadística, la formulación de hipótesis que implica dos variables (o la comparación de grupos) busca determinar si existen diferencias en una variable entre grupos y, de ser el caso, evaluar si esta diferencia es estadísticamente significativa.

Hasta ahora, hemos aprendido a contrastar hipótesis sobre diferencias entre grupos. A esto también se le llama hipótesis de dos colas.

Prueba de dos colas

Contrastamos la hipótesis nula (o de trabajo) de no diferencias entre grupos: \[ H_{0}: \mu_{1} - \mu_{2} = 0 \] En relación a una hipótesis alternativa sobre diferencias entre grupos: \[ H_{A}: \mu_{1} - \mu_{2} \neq 0 \]

Además, podemos plantear hipótesis respecto a que el valor de cierto parámetro para un grupo puede ser mayor o menor al de otro grupo. A esto se le conoce como hipótesis de una cola.

Prueba de una cola

\[ H_{0}: \mu_{0} ≥ \mu_{1} ; \mu_{0} ≤ \mu_{1}\]

\[ H_{A}: \mu_{0} > \mu_{1} \]

\[ H_{A}: \mu_{0} < \mu_{1} \]

Veamos ahora cómo aplicar todos estos conocimientos con ejercicios.

Ejercicio 1

Este ejercicio está basado en un ejemplo de clases y está desarrollado para que sirva de ejemplo a los siguientes ejercicios que deben ser desarrollados de manera autónoma.

La pregunta de investigación es: ¿Es el salario de los hombres mayor que el de las mujeres?

Para contrastar esta hipótesis, vamos utilizar la bbdd proc_casen, seleccionaremos las variables sexo e ytrabajocor y haremos un subset de datos de 1.500 casos.

casen_subset <- proc_casen %>% 
  select(sexo, ytrabajocor) %>% # seleccionamos
  sample_n(1500) # extraemos una muestra de 1500 casos

casen_subset <- na.omit(casen_subset) # eliminamos casos perdidos (listwise)

Generamos tabla para visualizar la distribución de los datos.

casen_subset %>% 
  dplyr::group_by(sexo) %>% # se agrupan por la variable categórica 
  dplyr::summarise(Obs. = n(),
                   Promedio = mean(ytrabajocor, na.rm=TRUE),
                   SD = sd(ytrabajocor, na.rm=TRUE)) %>% # se agregan las operaciones a presentar en la tabla
  kableExtra::kable(format = "markdown") # se genera la tabla

sexo	Obs.	Promedio	SD
1	347	818853.3	1032522.6
2	312	502896.2	378438.7

Ahora vamos con los 5 pasos de la inferencia

1. Formulación de hipótesis

El primer aspecto a establecer es el tipo de hipótesis a formular: ¿Direccional o no direccional? En este caso, la pregunta indica una direccionalidad (“mayor que”), por lo tanto corresponde a una hipótesis direccional. Si hubiera sido una pregunta que hiciera referencia simplemente a diferencias (“¿Es el salario de los hombres distinto al de las mujeres?”) correspondería a una hipótesis no direccional.

La hipótesis general es que el salario de los hombres es mayor que el de las mujeres. Pasando a lenguaje de hipótesis, esto se plantea como:

Hipótesis alternativa:

• \(H_A\): Promedio salarial hombres ( \(\bar{X}_{hombres}\)) - Promedio salarial mujeres ( \(\bar{X}_{mujeres}\)) > 0

Hipótesis nula:

• \(H_0\): \(\bar{X}_{hombres} - \bar{X}_{mujeres} \leq 0\)

Pasos 2, 3 y 4 de una vez con R

En clases vimos que los pasos 2, 3 y 4 corresponden a:

1. Obtener error estándar y estadístico de prueba empírico correspondiente (ej: Z o t)

2. Establecer la probabilidad de error \(\alpha\) (usualmente 0.05) y obtener valor crítico (teórico) de la prueba correspondiente

3. Cálculo de intervalo de confianza / contraste valores empírico/crítico

Esta secuencia de pasos tiene un sentido pedagógico para poder entender cómo finalmente se llega a interpretar el contraste de hipótesis en el paso 5. Pero en análisis de datos, luego de establecer las hipótesis nos vamos directamente al software que nos permite obtener de una vez toda la información de los pasos 2, 3 y 4.

test_ej1 <- t.test(casen_subset$ytrabajocor ~ casen_subset$sexo, 
                   alternative = "greater",
                   conf.level = 0.95)

test_ej1

    Welch Two Sample t-test

data:  casen_subset$ytrabajocor by casen_subset$sexo
t = 5.3169, df = 446.04, p-value = 0.00000008362
alternative hypothesis: true difference in means between group 1 and group 2 is greater than 0
95 percent confidence interval:
 218007.7      Inf
sample estimates:
mean in group 1 mean in group 2 
       818853.3        502896.2 

También podemos visualizarlo en una tabla más amable.

library(flextable)
library(rempsyc)
stats.table <- tidy(test_ej1, conf_int = T)
nice_table(stats.table, broom = "t.test")

Method	Alternative	Mean 1	Mean 2	M1 - M2	t	df	p	95% CI
Welch Two Sample t-test	greater	818,853.29	502,896.20	315,957.09	5.32	446.04	< .001***	[218007.71, Inf]

Visualicemos la distribución de esta prueba y su zona de rechazo.

gginference::ggttest(test_ej1)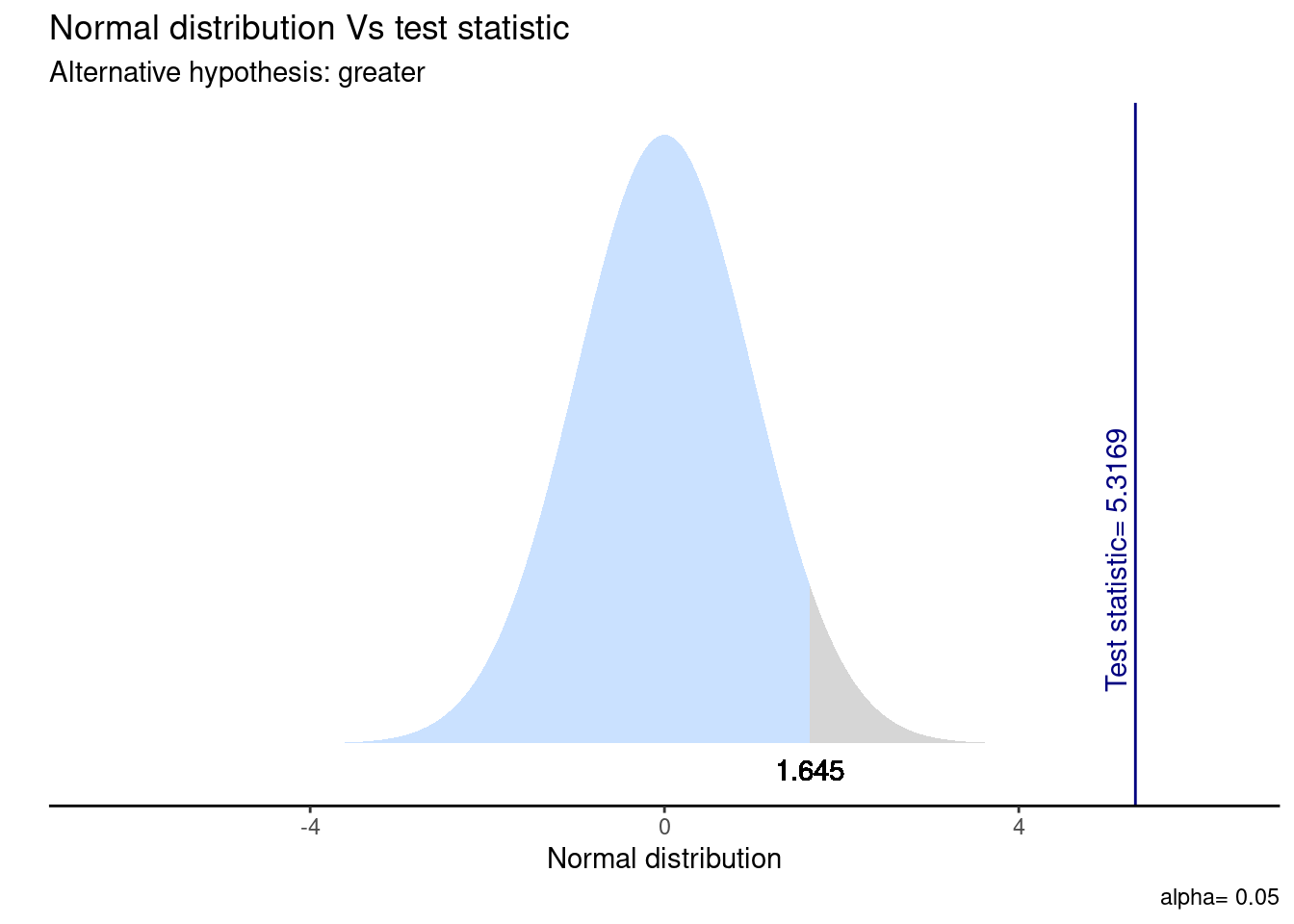

5. Interpretación

La prueba T que evalúa la diferencia de medias entre el salario y el sexo sugiere que el efecto es positivo y estadísticamente signficativo (diferencia = 32567.11, t(566.69) = 2.05, p < .05). El valor \(p\) indica que la probabilidad de observar una diferencia de esta magnitud, o mayor, bajo la suposición de \(H_{0}\) es menor al 5%. Por tanto, con un 95% de confianza, rechazamos la \(H_{0}\) ya que existe evidencia a favor de nuestra \(H_{A}\) respecto a que el salario de los hombres es mayor al salario de las mujeres.

Ejercicio 2

Tomando como ejemplo el trabajo de la ganadora del Premio Nobel de Economía 2023 Claudia Goldin, en este ejercicio evaluaremos la siguiente pregunta: ¿Es el salario de las mujeres sin hijos menor al salario de las mujeres con hijos? Por ende, usaremos prueba \(t\) para diferencia de medias.

Utilice la bbdd proc_casen y seleccione las variables ocupado, sexo, ytrabajocor e hijo. Luego, filtra por ocupado == 1 y sexo == 2 para quedarse solo con mujeres ocupadas y genera una muestra aleatoria de 1.500 casos con la función sample_n(). Luego, elimina los casos pérdidos con na.omit().

Genere una tabla de descriptivos de los ingresos (ytrabajocor) según si las observaciones tienen hijos o no (hijo). Presente cantidad de observaciones por categoría, media y desviación estándar.

Una ayuda con el procesamiento (solo esta vez)…

goldin_data <- proc_casen %>% 
  dplyr::select(ocupado, sexo, ytrabajocor, hijo) %>% 
  dplyr::filter(ocupado == 1 & sexo == 2) %>% 
  sample_n(1500) %>% 
  na.omit()# creamos subset con solo mujeres ocupadas

goldin_data %>% 
  dplyr::group_by(hijo) %>% 
  dplyr::summarise(Obs. = n(),
                   Media = mean(ytrabajocor, na.rm = T),
                   DS = sd(ytrabajocor, na.rm = T)) %>% 
  kableExtra::kable(format = "markdown") # hacemos la tabla

hijo	Obs.	Media	DS
0	376	650186.2	540687.7
1	1082	558742.2	498760.1

Ahora vamos con los 5 pasos de la inferencia

1. Formulación de hipótesis

El primer paso es traducir nuestra pregunta a una hipótesis estadística contrastable. Para ello: a) elija el tipo de hipótesis a plantear ¿direccional o no direccional? y b) especifique la hipótesis nula (\(H_0\)) e hipótesis alternativa (\(H_A\)).

Pasos 2, 3 y 4 de una vez con R

Siguiendo el ejemplo del Ejercicio 1, utilice el software para generar los estadísticos correspondientes. Contraste sus hipótesis considerando un 95% de confianza.

5. Interpretación

Interprete los resultados obtenidos: ¿es posible rechazar la hipótesis planteada?

La prueba T que evalúa la diferencia de medias…

Ejercicio 3

En este ejercicio tomamos de ejemplo una pregunta clásica en ciencias sociales: ¿el ingreso de las personas está relacionado a su nivel educacional?. Para responder esta pregunta vamos a usar una prueba \(t\) de contraste de medias para dos muestras independientes.

Esta vez les dejaremos el procesamiento a ustedes. Utilice la bbdd proc_casen y seleccione las variables ytrabajocor y universitaria. Luego genere una muestra aleatoria 1500 casos con la función sample_n() y elimine los datos perdidos de la variable ytrabajocor. Luego, genere una tabla de descriptivos de los ingresos (ytrabajocor) según si las personas cuentan con educación universitaria o no (universitaria). Presente cantidad de observaciones por categoría, media y desviación estándar.

1. Formulación de hipótesis

El primer paso es traducir nuestra pregunta a una hipótesis estadística contrastable. Para ello: a) elija el tipo de hipótesis a plantear ¿direccional o no direccional? y b) especifique la hipótesis nula (\(H_0\)) e hipótesis alternativa (\(H_A\)).

Pasos 2, 3 y 4 de una vez con R

Siguiendo el ejemplo del Ejercicio 1, utilice el software para generar los estadísticos correspondientes. Contraste sus hipótesis considerando un 95% de confianza y un 99% de confianza. Comente las diferencias en el paso 5.

5. Interpretación

Interprete los resultados obtenidos: ¿es posible rechazar la hipótesis nula? ¿a raíz de qué información llega a la conclusión? ¿qué diferencia observa al aplicar la prueba con ambos niveles de confianza (95% y 99%)?