Processing math: 35%
+ - 0:00:00
Notes for current slide
Notes for next slide

Estadística Correlacional

Inferencia, asociación y reporte

Juan Carlos Castillo

Sociología FACSO - UChile

2do Sem 2024

correlacional.netlify.app

Sesión 9:

Inferencia en correlación y magnitud del coeficiente

1 / 36

Lecturas

- Pardo 307 - 330 Relación lineal

- Huck 183 - 203 Statistical Inferences Concerning Bivariate Correlation Coefficients

2 / 36

1- Resumen sesión anterior

2- Inferencia en correlación

3- Magnitud del coeficiente de correlación

3 / 36


id educ ing
1 2 1
2 3 3
3 4 3
4 4 5
5 5 4
6 7 7
7 8 9
8 8 11

4 / 36

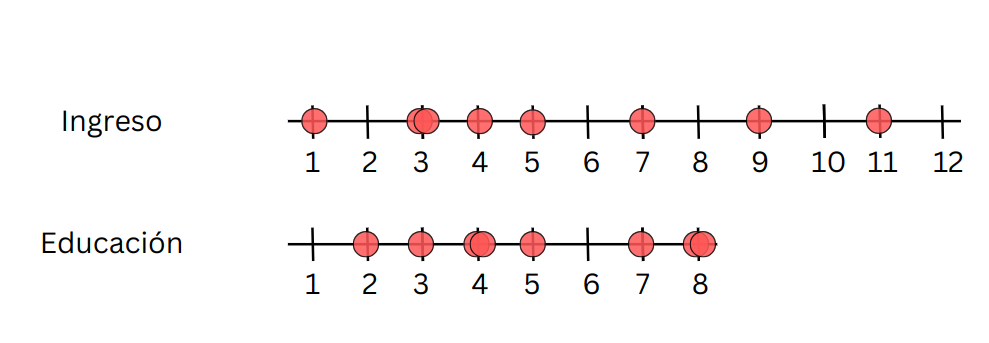
Varianzas

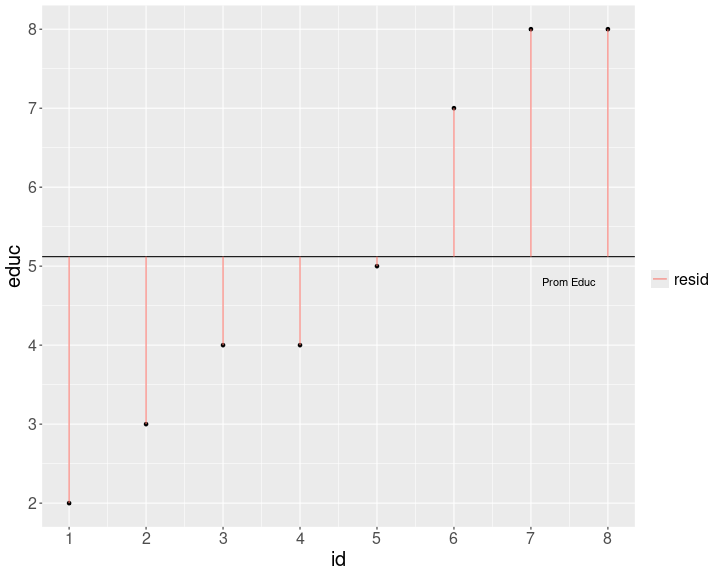
Educación

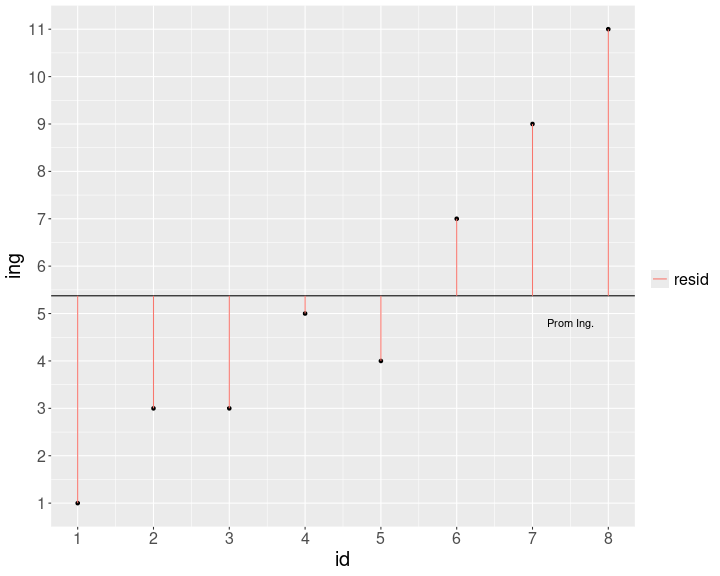
Ingreso

5 / 36

Nube de puntos

6 / 36

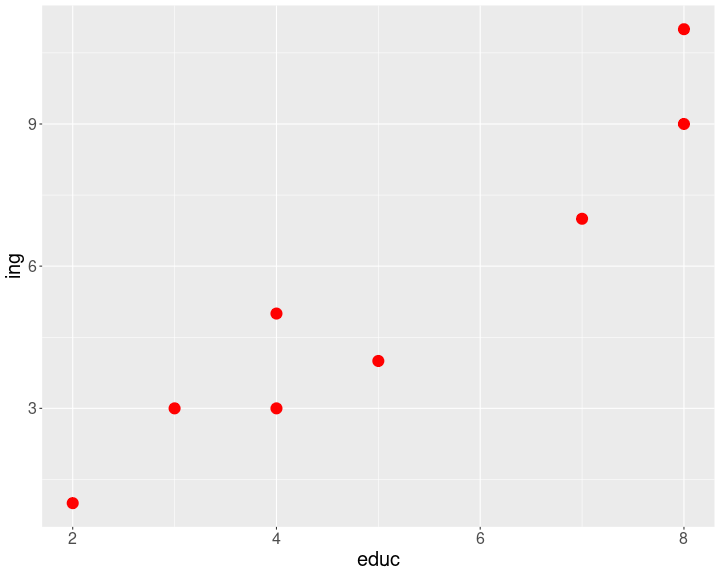
Covarianza

Varianza educación (x)

σ2edu=∑Ni=1(xi−ˉx)2N−1 σ2edu=∑Ni=1(xi−ˉx)(xi−ˉx)N−1

Varianza ingreso (y)

σ2ing=∑Ni=1(yi−ˉy)2N−1 σ2ing=∑Ni=1(yi−ˉy)(yi−ˉy)N−1

7 / 36

Covarianza

Varianza educación (x)

σ2edu=∑Ni=1(xi−ˉx)2N−1 σ2edu=∑Ni=1(xi−ˉx)(xi−ˉx)N−1

Varianza ingreso (y)

σ2ing=∑Ni=1(yi−ˉy)2N−1 σ2ing=∑Ni=1(yi−ˉy)(yi−ˉy)N−1

Covarianza=cov(x,y)=∑Ni=1(xi−ˉx)(yi−ˉy)N−1

7 / 36

Covarianza

  • valor numérico que refleja la asociación entre dos variables

  • el signo indica si la asociación es positiva o negativa

  • valor no interpretable directamente, depende de valores de cada variable

8 / 36

Covarianza

  • valor numérico que refleja la asociación entre dos variables

  • el signo indica si la asociación es positiva o negativa

  • valor no interpretable directamente, depende de valores de cada variable

Correlación

  • valor numérico que refleja la asociación entre dos variables

  • el signo indica si la asociación es positiva o negativa

  • rango de variación fijo entre -1 y +1, interpretable en términos de magnitud

8 / 36

Cálculo correlación

educ ing dif_m_educ2 dif_m_ing2 dif_xy
2 1 9.77 19.14 13.67
3 3 4.52 5.64 5.05
4 3 1.27 5.64 2.67
4 5 1.27 0.14 0.42
5 4 0.02 1.89 0.17
7 7 3.52 2.64 3.05
8 9 8.27 13.14 10.42
8 11 8.27 31.64 16.17

r=∑(x−ˉx)(y−ˉy)√∑(x−ˉx)2∑(y−ˉy)2

sum(data$dif_xy); sum(data$dif_m_educ2);sum(data$dif_m_ing2)
[1] 51.625
[1] 36.875
[1] 79.875
9 / 36

Cálculo correlación

r=∑(x−ˉx)(y−ˉy)√∑(x−ˉx)2∑(y−ˉy)2=51.625√36.875∗79.875=51.62554.271=0.951

10 / 36

Cálculo correlación

r=∑(x−ˉx)(y−ˉy)√∑(x−ˉx)2∑(y−ˉy)2=51.625√36.875∗79.875=51.62554.271=0.951

cor(data$educ,data$ing)
[1] 0.9512367
10 / 36

Interpretación

  • El coeficiente de correlación (de Pearson) es una medida de asociación lineal entre variables, que indica el sentido y la fuerza de la asociación
11 / 36

Interpretación

  • El coeficiente de correlación (de Pearson) es una medida de asociación lineal entre variables, que indica el sentido y la fuerza de la asociación

  • Varía entre +1 y -1, donde

    • valores positivos indican relación directa (aumenta una, aumenta la otra)

    • valores negativos indican relación inversa (aumenta una, disminuye la otra)

11 / 36

Nubes de puntos (scatterplot) y correlación

12 / 36

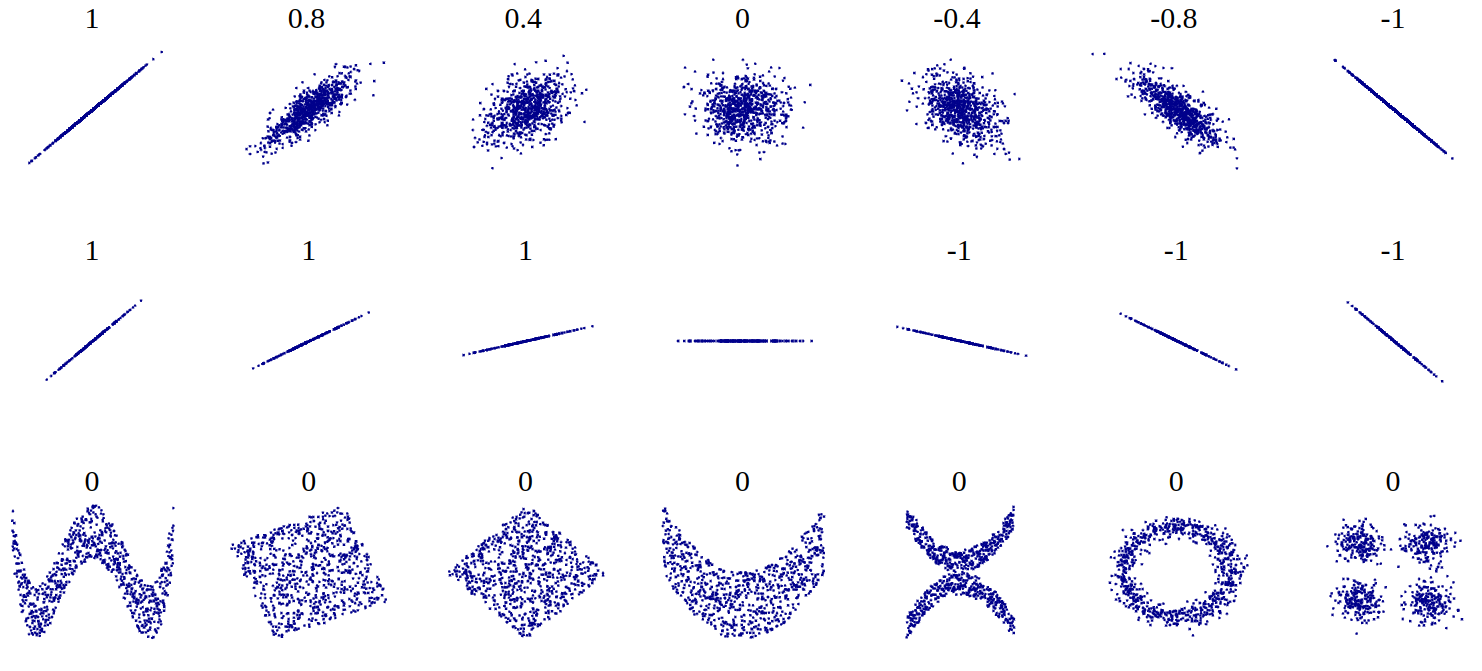
1- Resumen sesión anterior

2- Inferencia en correlación

3- Magnitud del coeficiente de correlación

13 / 36

Datos

Simulamos dos variables: edad, y puntaje en escala de izquierda (1) - derecha (10):

edad <-c(18,25,40,55,70, 82)
iz_der <-c(5,4,5,9,5,7)
cor(edad,iz_der)
[1] 0.5070278
(cor(edad,iz_der))^2 #r2
[1] 0.2570772
14 / 36
plot1 <- ggplot(, 
  aes(x=edad, y=iz_der)) + 
  geom_point(
    colour = "red", 
    size = 5) +
  theme(text = 
    element_text(size = 20))
plot1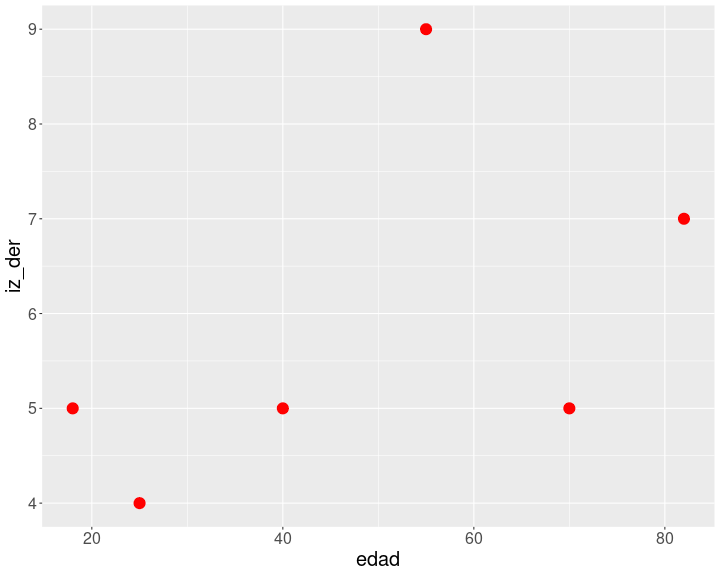

15 / 36

Prueba de hipótesis de correlación

1. Formulación de hipótesis

Siendo ρ (rho) la correlación r en la población:

H0:ρ=0 Ha:ρ≠0

16 / 36

La hipótesis de correlación refiere a asociación, no a explicación ni a causalidad

17 / 36

Prueba de hipótesis de correlación

2. Error estándar y estadístico de prueba ( t)

\begin{align*} SE_r=&\sqrt{\frac{1-r²}{n-2}} \\\\ =&\sqrt{\frac{1-0.257}{6-2}} \\\\ =&\sqrt{\frac{0.743}{4}}=\sqrt{0.186}=0.431 \end{align*}

\begin{align*} t_r&=\frac{r}{SE_r} \\\\ &=\frac{0.51}{0.431} \\\\ &=1.18 \end{align*}

18 / 36

Prueba de hipótesis de correlación

3. Probabilidad de error y valor crítico para t

  • para un nivel de error \alpha=0.05

  • y una hipótesis de diferencia de dos colas: \alpha/2=[0.025-0.975]

  • grados de libertad N-2= 6-2 = 4

qt(p=.05/2, 
   df=4, 
   lower.tail=FALSE)
[1] 2.776445
19 / 36

Prueba de hipótesis de correlación

4. Contraste de valores empírico y crítico

  • Contraste: t_{r}=1.18 < t_{cri}=2.77
20 / 36

Prueba de hipótesis de correlación

4. Contraste de valores empírico y crítico

  • Contraste: t_{r}=1.18 < t_{cri}=2.77

5. Interpretación

Nuestro t estimado es menor que el valor t crítico para un 95% de confianza, por lo tanto no rechazamos la hipótesis nula. No existe evidencia en nuestros datos para afirmar que la correlación entre la escala izquierda-derecha y edad es distinta de cero en la población.

20 / 36

En R

cor.test(iz_der,edad)
    Pearson's product-moment correlation
data:  iz_der and edad
t = 1.1765, df = 4, p-value = 0.3046
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.5174601  0.9341863
sample estimates:
      cor 
0.5070278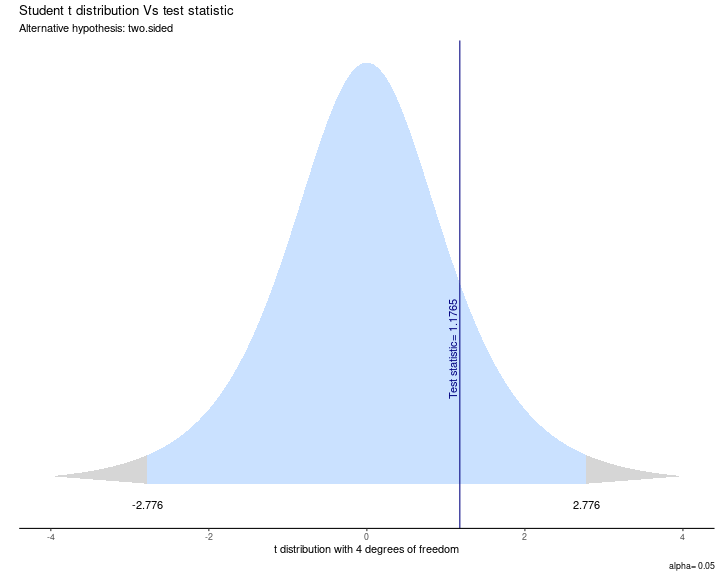
21 / 36

22 / 36

1- Resumen sesión anterior

2- Inferencia en correlación

3- Magnitud del coeficiente de correlación

23 / 36

Si dos variables covarían, entonces comparten varianza

24 / 36

Si dos variables covarían, entonces comparten varianza

¿Cuánta varianza comparten?

24 / 36

Estableciendo la varianza compartida

La varianza compartida puede pensarse como 1 - la varianza no compartida (o varianza única)

La varianza no compartida se asocia al concepto de residuos, es decir, la cantidad de varianza que no está contenida en la correlación

25 / 36

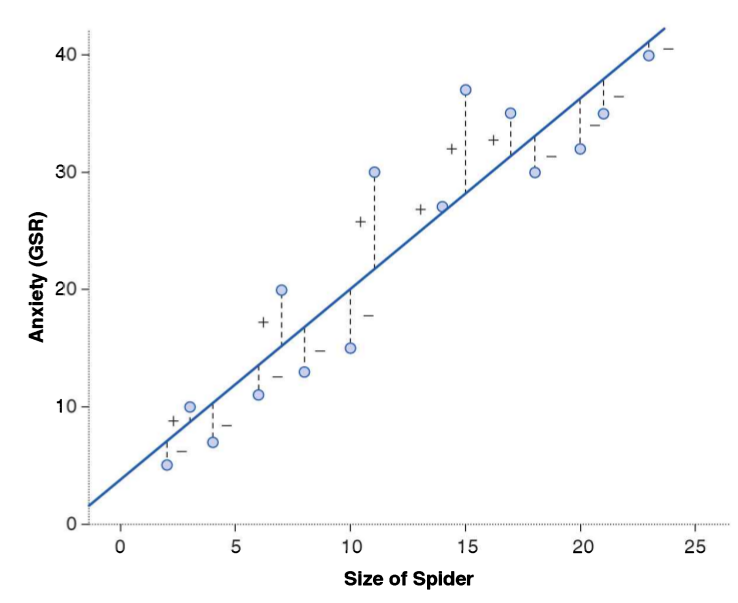
Estableciendo la varianza compartida

Para poder obtener los residuos vamos a generar una recta que represente la asociación entre las variables. Esta es la recta de regresión 1

Esta recta nos permite obtener un valor estimado de y para cada valor de x








[1] Detalles próximo semestre

26 / 36
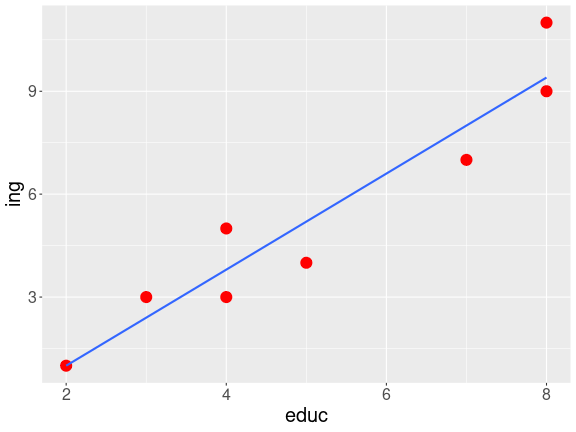
reg1 <- lm(ing ~ educ, data=data)
data$predict <-predict.lm(reg1) 
plot2 <-ggplot(data, 
  aes(x=educ, y=predict)) + 
  geom_point(
    colour = "red", 
    size = 5) +
  theme(text = 
    element_text(size = 20))+
  stat_smooth(method = "lm", 
    se = FALSE, fullrange = T)
plot2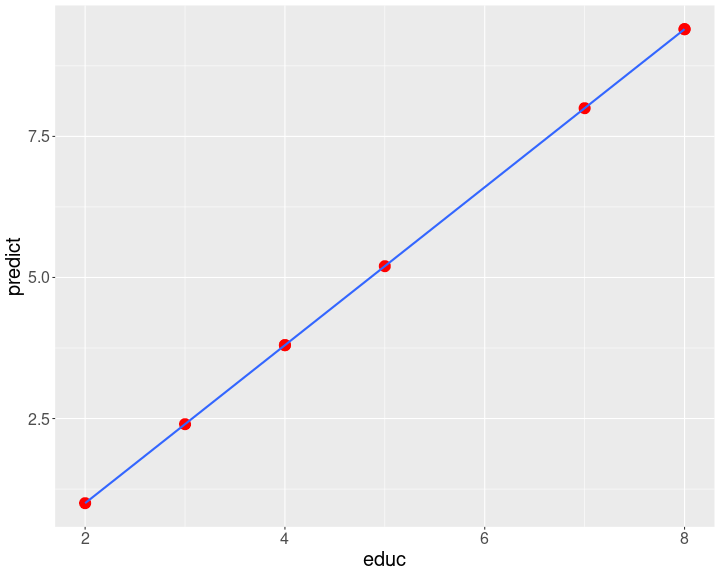

27 / 36

\begin{align*} SS_{tot}&=SS_{reg} + SS_{error} \\ \Sigma(y_i - \bar{y})^2&=\Sigma (\hat{y}_i-\bar{y})^2 +\Sigma(y_i-\hat{y}_i)^2 \end{align*}

28 / 36

Varianza compartida

SS_{tot}=SS_{reg} + SS_{error}

29 / 36

Varianza compartida

SS_{tot}=SS_{reg} + SS_{error}

\frac{SS_{tot}}{SS_{tot}}=\frac{SS_{reg}}{SS_{tot}} + \frac{SS_{error}}{SS_{tot}}

29 / 36

Varianza compartida

SS_{tot}=SS_{reg} + SS_{error}

\frac{SS_{tot}}{SS_{tot}}=\frac{SS_{reg}}{SS_{tot}} + \frac{SS_{error}}{SS_{tot}}

1=\frac{SS_{reg}}{SS_{tot}}+\frac{SS_{error}}{SS_{tot}}

\frac{SS_{reg}}{SS_{tot}}= 1- \frac{SS_{error}}{SS_{tot}}=R^2

29 / 36

¿Qué relación tienen R^2 y r (correlación)?

R^2=r^2

Por lo tanto, en nuestro ejemplo:

cor(data$educ,data$ing)
[1] 0.9512367
\begin{align*} r&= 0.95 \\ r^2&=0.95 ^2 \\ r^2&=0.902 = R^2 \end{align*}
30 / 36

¿Qué relación tienen R^2 y r (correlación)?

R^2=r^2

Por lo tanto, en nuestro ejemplo:

cor(data$educ,data$ing)
[1] 0.9512367
\begin{align*} r&= 0.95 \\ r^2&=0.95 ^2 \\ r^2&=0.902 = R^2 \end{align*}

Intepretación:

El porcentaje de varianza compartida entre educación e ingreso es de 90%.

Es decir, ambas variables comparten el 90% de su varianza

30 / 36

R^2 o coeficiente de determinación

  • ¿Cuánto de los ingresos se asocia a educación, y viceversa?
31 / 36

R^2 o coeficiente de determinación

  • ¿Cuánto de los ingresos se asocia a educación, y viceversa?

  • el R^2

    • es la proporción de la varianza de Y que se asocia a X

    • varía entre 0 y 1, y usualmente se expresa en porcentaje

31 / 36

Tamaños de efecto

32 / 36

Criterios de Cohen para tamaños de efecto

  • El coeficiente de correlación r de Pearson nos indica la dirección y la fuerza/intensidad de la asociación.

  • Pero, ¿qué nos dice el tamaño del coeficiente? Por ejemplo, si el coeficiente es 0.5, ¿esto es pequeño, mediano o grande?

33 / 36

Criterios de Cohen para tamaños de efecto

  • El coeficiente de correlación r de Pearson nos indica la dirección y la fuerza/intensidad de la asociación.

  • Pero, ¿qué nos dice el tamaño del coeficiente? Por ejemplo, si el coeficiente es 0.5, ¿esto es pequeño, mediano o grande?

  • Cohen (1988, 1992) sugiere una serie de criterios convencionales para clasificar efectos como pequeños, medianos o grandes.

33 / 36

Para el caso de correlación de Pearson, Cohen sugiere:

  • tamaño de efecto pequeño: alrededor de 0.10

  • tamaño de efecto mediano: alrededor de 0.30

  • tamaño de efecto grande: alrededor de 0.50 y más

34 / 36

Resumen

  • Inferencia en correlación: contraste con valor crítico t

  • Coeficiente de determinación R^2: varianza compartida entre variables

  • Tamaño de efecto: valores convencionales para establecer si una magnitud es pequeña, mediana o grande.

35 / 36

Estadística Correlacional

Inferencia, asociación y reporte

Juan Carlos Castillo

Sociología FACSO - UChile

2do Sem 2024

correlacional.netlify.app

36 / 36

Lecturas

- Pardo 307 - 330 Relación lineal

- Huck 183 - 203 Statistical Inferences Concerning Bivariate Correlation Coefficients

2 / 36
Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow