class: front .pull-left-wide[ # Estadística Correlacional] .pull-right-narrow[] ## Inferencia, asociación y reporte ---- .pull-left[ ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 2do Sem 2024 ## [.orange[correlacional.netlify.com]](https:/correlacional.netlify.com) ] .pull-right-narrow[ .center[ .content-block-gray[ ## .gray[Sesión 4:] ## .curso[Inferencia 3: Intervalos de confianza]] ] ] --- layout: true class: animated, fadeIn --- # Pilares de la inferencia .pull-left[ ### Curva normal 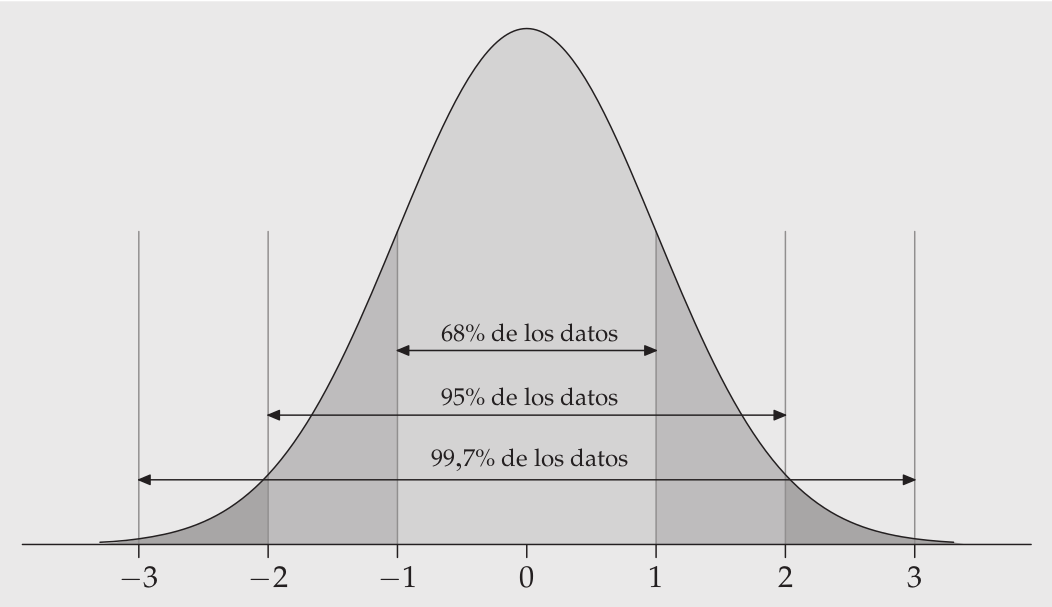 ] .pull-right[ ### Error estándar `$$\sigma_{\bar{X}}=SE(error estándar)=\frac{s}{\sqrt{N}}$$` ] --- # Diferencias desviación estándar y error estándar .pull-left[ ### Desviación estándar # `\(\sigma=\sqrt{\frac{\Sigma(x_i-\bar{X})²}{N-1}}\)` Magnitud que expresa la dispersión en torno al promedio en la escala de la variable ] .pull-right[ ### Error estándar (del promedio) ## `$$\sigma_{\bar{X}}=SE=\frac{s}{\sqrt{N}}$$` .medium[Magnitud que equivale a la desviación estándar de los promedios de varias muestras] ] --- ## ... y más de Error Estándar - se calcula no solo para el promedio, sino para **distintos estadísticos** como correlación, regresión, desviación estándar (con distintas fórmulas para cada uno) - como está expresado en unidades estándar de variación, permite construir **rangos de probabilidad** basados enla distribución normal - estos rangos de probabilidad se conocen como **intervalos de confianza** --- class: inverse bottom right # Intervalos de confianza --- - El error estándar, por su asociación a las áreas de la curva normal, se relaciona con **niveles de probabilidad** - Si sumo y resto error(es) estándar al promedio puedo construir un rango de valores probables en que se encuentra el parametro poblacional -> **intervalo de confianza** - Por ejemplo, si tengo un promedio=10 y SE=1, puedo decir que aproximadamente el 68% de los casos se encuentran en el **intervalo** entre 9 y 11 (basado en distribución normal) -- .content-box-red[ .center[Pero ... ¿Es suficiente un rango que cubra al 68%] ] --- # Error y confianza - Un 68% implica que la probabilidad de que el promedio esté fuera de ese rango (o **probabilidad de error**) es de un 32% (100%-68%) -- .center[ .content-box-red[ ## ¿Es aceptable este nivel? ]] -- Esto es equivalente a preguntarse cuánto error estoy dispuesto a tolerar como resultado de una inferencia estadística -- Y se asocia al concepto de **.red[nivel de confianza**] --- # ¿Certeza o precisión? - No hay certezas, solo probabilidades - Las probabilidades se asocian a un rango (intervalo) que garantice un cierto nivel de confianza - Y esto requiere un compromiso o compensación (trade-off), ya que: .medium[ - un intervalo mayor poseerá un mayor nivel de confianza, pero en un rango de valores demasiado amplio - un intervalo menor poseerá un menor nivel de confianza, pero en un rango de valores más estrecho ] --- # Es decir, qué tipo de conclusión prefiero: - el promedio de ingresos se encuentra entre 500.000 y 5.000.000, con un 99% de confianza, ó - el promedio de ingresos se encuentra entre 700.000 y 710.000, con un 65% de confianza -- .content-box-red[ .center[ _.red["con un 100% de probabilidad te aseguro que tu nota se encuentra entre 1 y 7"]_]] --- # Intervalos vs confianza  --- # ¿De qué depende el nivel de confianza? - en estadística inferencial, la confianza se asocia a 1 - probabilidad de error - la probabilidad de error a aceptar no es un criterio estadístico, es convencional - por convención, se acepta como estadísticamente significativa una probabilidad de error **menor al 5%**, lo que equivale (al menos) a un **nivel de confianza del 95%** --- # ¿Qué significa un 95% de confianza? - que si tuviéramos la posibilidad de extraer múltiples muestras, el 95% de las veces nuestro intervalo contendría el promedio -- - o que existe un 5% de probabilidad de error, es decir, de que el promedio de la muestra no sea el de la población -- - o que las chances de error son 1 de 20 --- .center[  ] --- class: roja # Un .yellow[intervalo de confianza] (IC o CI) es la mejor estimación del rango de un estadístico en la población (parámetro poblacional) con una muestra aleatoria --- class: inverse middle ## ¿De qué depende el .red[tamaño] del intervalo de confianza? ## ¿Cómo se establece el .red[nivel de confianza] del intervalo? --- ## ¿De qué depende el tamaño del intervalo de confianza? - recordemos que el intervalo de confianza se elabora sumando y restando errores estándar al promedio `$$\sigma_{\bar{X}}=SE(error estándar)=\frac{s}{\sqrt{N}}$$` -- - dado que el tamaño muestral (N) se encuentra en el denominador del `\(SE\)`, a mayor N, menor será el `\(SE\)` y menor el intervalo de confianza - esto tiene implicancias directas en el cálculo del tamaño muestral --- # Pasos en la construcción del intervalo de confianza (para un promedio) 1. Obtención de la media y el error estándar 2. Determinar el nivel de confianza (expresado en puntaje Z) para la construcción del intervalo 3. Aplicar fórmula: `$$\bar{X}\pm Z*\frac{\sigma}{\sqrt{N}}$$` --- # Determinando el nivel de confianza .pull-left-narrow[ .medium[ - Nuestro promedio muestral `\(\bar{x}\)` posee una distribución normal con una desviación estandar = SE (error estándar) - Esto nos permite estimar probabilidades basados en los valores de la curva normal ] ] .pull-right-wide[ .center[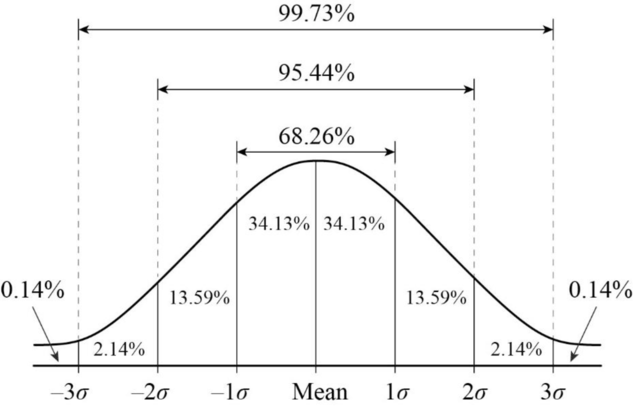]] --- # Valores del intervalo Determinar el valor del límite superior y el límite inferior del intervalo en la curva normal para un nivel de confianza del 95%: .center[  ] --- # Valores del intervalo .pull-left[ El límite inferior de un intervalo al 95% de confianza corresponde al percentil 2,5%, y el límite superior al 97,5% (95% + 2,5%) ] .pull-right[  ] --- Y sabemos por la distribución normal que entre +/- 2 desviaciones estándar de la curva normal se encuentra el 95,44% de los casos: .center[] Por lo tanto, para un 95% será algo menos que +/- 2ds ... pero cuánto específicamente? --- # De percentil a puntaje Z .pull-left[ Recordemos que al calcular el puntaje Z, el resultado se expresa en desviaciones estándar de la curva normal, lo que puede ser transformado a percentiles. Por lo tanto, se puede hacer la operación inversa -> a que puntaje Z corresponde un determinado percentil ] .pull-right[ 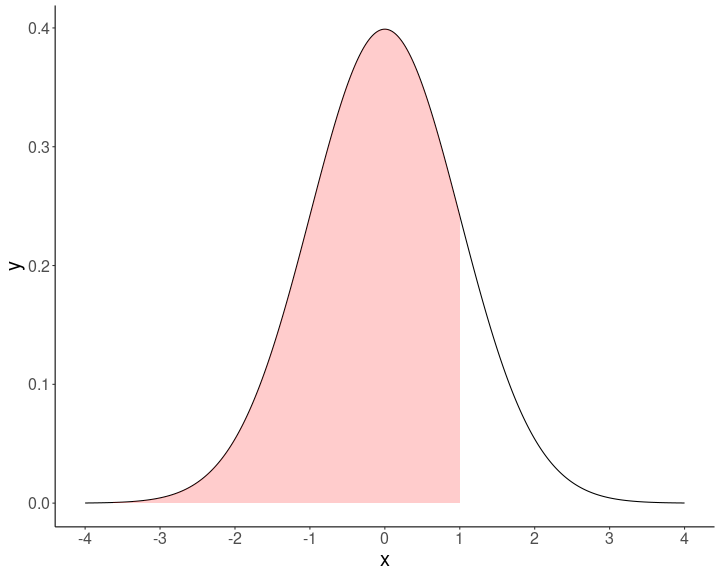 ] --- - Para hacer la equivalencia entre puntajes Z y percentiles vamos a una tabla de puntajes Z ... o directamente en R: ``` r qnorm(0.025) # límite inferior ``` ``` [1] -1.959964 ``` ``` r qnorm(0.975) # límite superior ``` ``` [1] 1.959964 ``` Y aproximando: `\(\pm{1.96}\)`. Por lo tanto: --- class: inverse middle center .center[ .red[ # Sumando y restando **1.96** errores estándar al promedio construimos un intervalo de confianza del 95%] ] --- ## Intervalo de 95% de confianza .pull-left[ .center[]] .pull-right[ .medium[ - El valor de Z que deja el 2.5% de probabilidad en la cola izquierda y el 2.5% en la derecha es aproximadamente ±1.96 - Un intervalo de confianza de `\(\bar{x}\pm1.96SE\)` abarca aproximadamente el 95% de los valores probables - En este caso, puedo decir que el promedio se encuentra en un rango de valores con un .red[nivel de confianza] de 95% ] ] --- ## Ejemplo: intervalo de confianza para un promedio ---- .pull-left[ .content-box-green[ - Tenemos: - promedio de ingresos: 800.000 - desviación estándar: 100.000 - N muestral: 1.600 ]] .pull-right[ `\begin{align*} SE&=\frac{s}{\sqrt{N}} \\\\ &=\frac{100.000}{\sqrt{1.600}} \\\\ &=\frac{100.000}{40}=2.500 \end{align*}` ] --- - Tenemos: `\(SE=2.500\)`, `\(\bar{x}_{ingresos}=800.000\)` - Con estos valores podemos construir un rango de probabilidad basado en la curva normal, sumando y restando errores estándar - `\(\bar{X}{\color{red}\pm}1.96SE\)` abarcan el 95% de los valores alrededor del promedio - `\(800.000 - (1.96*2.500) = 800.000 - 4.900={\color{red}{795.100}}\)` - `\(800.000 + (1.96*2.500) = 800.000 + 4.900={\color{red}{804.900}}\)` - Por lo tanto, podemos decir .red[con un 95% de confianza] que el promedio de ingresos se encuentra entre 795.100 y 804.900 --- # Aumentando el nivel de confianza: 99% - además del 95% de confianza, otro nivel convencional es el 99% de confianza - con este nivel tenemos una menor probabildad de error, pero un intervalo más grande - en este caso, el límite inferior del intervalo es 0.5%, y el superior 99.5% --- # En R Estimando valores Z para límites de intervalo de confianza al 99%: ``` r qnorm(0.005) # límite inferior ``` ``` [1] -2.575829 ``` ``` r qnorm(0.995) # límite superior ``` ``` [1] 2.575829 ``` --- # Generalizando: - Para un intervalo de confianza al 95%: # `\(\bar{X}\pm1.96SE\)` - Para un intervalo de confianza al 99%: # `\(\bar{X}\pm2.58SE\)` --- ## Mismo ejemplo, pero al 99% de confianza ---- .pull-left[ .content-box-green[ - Tenemos: - promedio de ingresos: 800.000 - desviación estándar: 100.000 - N muestral: 1.600 ]] .pull-right[ `\begin{align*} SE&=\frac{s}{\sqrt{N}} \\\\ &=\frac{100.000}{\sqrt{1.600}} \\\\ &=\frac{100.000}{40}=2.500 \end{align*}` ] --- - Tenemos: `\(SE=2.500\)`, `\(\bar{x}_{ingresos}=800.000\)` - `\(\bar{X}{\color{red}\pm}2.58SE\)` abarcan el 99% de los valores alrededor del promedio - `\(800.000 - (2.58*2.500) = 800.000 - 6.450={\color{red}{793.550}}\)` - `\(800.000 + (2.58*2.500) = 800.000 + 6.450={\color{red}{806.450}}\)` - Por lo tanto, podemos decir .red[con un 99% de confianza] que el promedio de ingresos se encuentra entre 793.550 y 806.450 --- # Comparando intervalos: - 95% de confianza: `\(800.000\pm4.900=[795.100 - 804.900]\)` - 99% de confianza: `\(800.000\pm6.450=[793.550 - 806.450]\)` Por lo tanto, a mayor nivel de confianza, mayor es el intervalo, pero disminuye la precisión o aumenta el **margen de error** --- # Margen de error - El margen de error es el valor en que puede oscilar el promedio en el intervalo. - Es decir, equivale a lo que se suma/resta al promedio para generar el intervalo, pero en general se expresa en términos de porcentaje --- # Ejemplo margen de error - Para nuestro intervalo al 95%, el margen de error equivale a qué porcentaje es 4.900 en relación al total. Aplicando regla de 3 para porcentajes: `\(Margen-error_{95}=\frac{4.900*100}{800.000}=0.612\)` - Por lo tanto, el margen de error en este caso es de `\(\pm{0.6}\%\)` --- class: inverse ## .yellow[Resumen] - definición de intervalo de confianza - cálculo e interpretación del intervalo de confianza - comparación de intervalos con distinto nivel de confianza - margen de error --- # Recomendaciones Ver [simulación de intervalo de confianza para promedio muestral](https://shiny.rit.albany.edu/stat/confidence/) --- class: front .pull-left-wide[ # Estadística Correlacional] .pull-right-narrow[] ## Inferencia, asociación y reporte ---- .pull-left[ ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 2do Sem 2024 ## [.orange[correlacional.netlify.com]](https://encuestas-sociales.netlify.com) ]