Estadística Correlacional
Inferencia, asociación y reporte
Inferencia 1:
Datos, probabilidad y distribuciones muestrales
Objetivos de la sesión de hoy
1. Recordar y nivelar aprendizajes previos a este curso, fundamentalmente respecto al manejo de datos, medición y varianza
2. Introducción a probablidad, distribuciones muestrales e inferencia
Contenidos
Bases
Probabilidad e inferencia
Contenidos
Bases
Probabilidad e inferencia
Datos
- Los datos son una expresión numérica de la medición de al menos una característica de a lo menos una unidad en a lo menos un punto en el tiempo
Datos
Los datos son una expresión numérica de la medición de al menos una característica de a lo menos una unidad en a lo menos un punto en el tiempo
- Ejemplo: La esperanza de vida en Chile el 2017 fue de 79,9 años
Característica (variable) : esperanza de vida
Unidad: Años
Punto en el tiempo: 2017
Medir
“asignar números, símbolos o valores a las propiedades de objetos o eventos de acuerdo con reglas” (Stevens, 1951)
Vincula conceptos abstractos con indicadores empíricos

Medir: requisitos básicos
Exhaustividad: el mayor número de categorías significativas.
- Ej: ¿Qué categorías se deben considerar para población migrante?
Exclusividad: atributos mutuamente excluyentes
Ejemplos de estudios / bases de datos
Variables
Una variable representa cualquier cosa o propiedad que varia y a la cuál se le asigna un valor. Es decir:
Variable≠ConstanteVariable≠Constante
Pueden ser visibles o no visibles/latentes. (Ej: peso / inteligencia)
Variables
discretas (Rango finito de valores):
- Dicotómicas
- Politómicas
continuas:
- Rango (teóricamente) infinito de valores.
Tendencia Central
Descripción básica de una variable:
Moda: valor que ocurre más frecuentemente
Mediana: valor medio de la distribución ordenada. Si N es par, entonces es el promedio de los valores medios
Media o promedio aritmético: suma de los valores dividido por el total de casos
Pregunta de tendencia central:
¿Puede la mayoría ganar menos ingresos que el promedio?
Dispersión:
Varianza
Dispersión:
Varianza
Dispersión:
Varianza
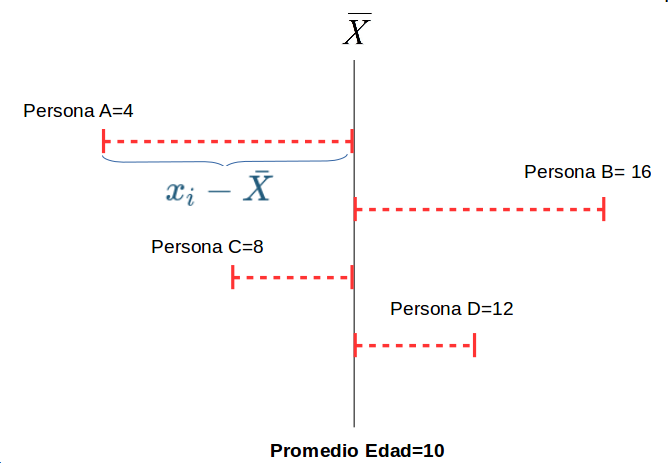
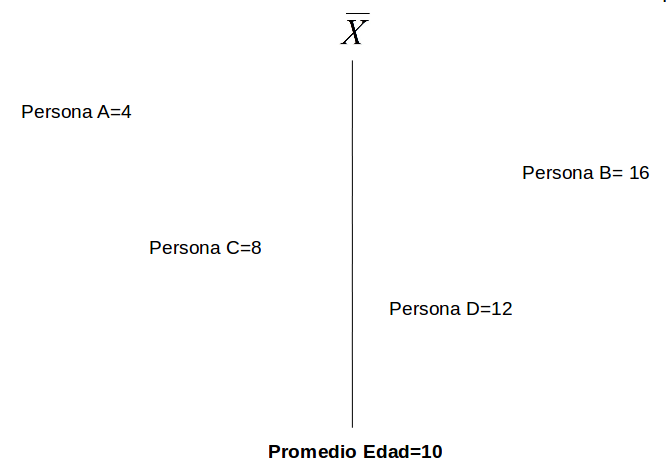
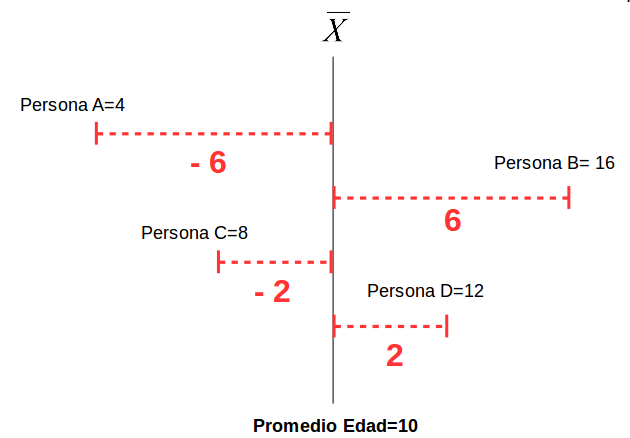
Dispersión:
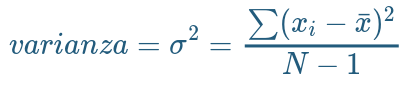
La VARIANZA equivale al promedio de la suma de las diferencias del promedio al cuadrado
Desviación Estándar
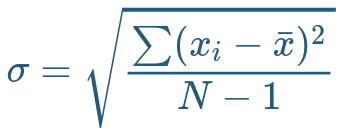
- Raiz Cuadrada de la varianza.
- Expresada en la mismas unidades que los puntajes de la escala original
Contenidos
Bases
Probabilidad e inferencia
Inferencia: la otra parte del análisis
Cuando se analizan datos, 2 cosas principales
cálculo del estadístico:
promedio
desviación estándar
correlación
...
inferencia: ¿existe este estadístico en la población?
probabilidad
error
significación
Inferencia
¿En qué medida se pueden relacionar resultados que se encuentran en un (sub)conjunto de unidades con lo que ocurre en general?
Inferencia
¿En qué medida se pueden relacionar resultados que se encuentran en un (sub)conjunto de unidades con lo que ocurre en general?
Ej: si en un subconjunto de la población encuentro que el promedio de matemáticas es mayor en mujeres que en hombres ¿es esto un reflejo de lo que ocurre en general, o se debe solo al azar? ¿se puede extrapolar a la poblacion?
mapa y territorio, Borges lidiando con el caos y la incertidumbre la domesticación de la casualidad error
En aquel Imperio, el Arte de la Cartografía logró tal Perfección que el mapa de una sola Provincia ocupaba toda una Ciudad, y el mapa del Imperio, toda una Provincia. Con el tiempo, estos Mapas Desmesurados no satisficieron y los Colegios de Cartógrafos levantaron un Mapa del Imperio, que tenía el tamaño del Imperio y coincidía puntualmente con él.
Menos Adictas al Estudio de la Cartografía, las Generaciones Siguientes entendieron que ese dilatado Mapa era Inútil y no sin Impiedad lo entregaron a las Inclemencias del Sol y los Inviernos. En los desiertos del Oeste perduran despedazadas Ruinas del Mapa, habitadas por Animales y por Mendigos; en todo el País no hay otra reliquia de las Disciplinas Geográficas.
Suárez Miranda, Viajes de Varones Prudentes, Libro Cuarto, Cap. XLV, Lérida, 1658.
En aquel Imperio, el Arte de la Cartografía logró tal Perfección que el mapa de una sola Provincia ocupaba toda una Ciudad, y el mapa del Imperio, toda una Provincia. Con el tiempo, estos Mapas Desmesurados no satisficieron y los Colegios de Cartógrafos levantaron un Mapa del Imperio, que tenía el tamaño del Imperio y coincidía puntualmente con él.
Menos Adictas al Estudio de la Cartografía, las Generaciones Siguientes entendieron que ese dilatado Mapa era Inútil y no sin Impiedad lo entregaron a las Inclemencias del Sol y los Inviernos. En los desiertos del Oeste perduran despedazadas Ruinas del Mapa, habitadas por Animales y por Mendigos; en todo el País no hay otra reliquia de las Disciplinas Geográficas.
Suárez Miranda, Viajes de Varones Prudentes, Libro Cuarto, Cap. XLV, Lérida, 1658.
Borges - Del Rigor de la Ciencia
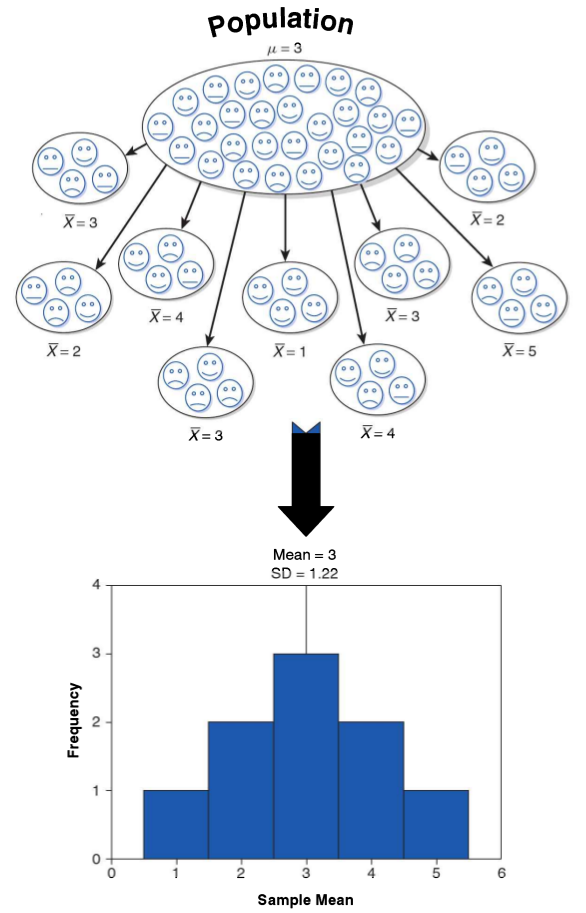
Conceptos claves de inferencia
- La inferencia en estadística se refiere a la relación que existe entre los resultados obtenidos basados en nuestra muestra y la población

Conceptos claves de inferencia
- La inferencia en estadística se refiere a la relación que existe entre los resultados obtenidos basados en nuestra muestra y la población
- ¿En qué medida podemos hacer inferencias desde nuestra muestra a la población?

Conceptos claves de inferencia
- La inferencia en estadística se refiere a la relación que existe entre los resultados obtenidos basados en nuestra muestra y la población
- ¿En qué medida podemos hacer inferencias desde nuestra muestra a la población?
- Un concepto central es la probabilidad de ERROR
Parámetros y estadísticos
| Población (parámetro) | Muestra (estadístico) | |
|---|---|---|
| Promedio | μμ | ˉx¯x |
| Varianza | σ²σ² | s²s² |
| Desviación estándar | σσ | ss |
| Correlación | ρρ | rr |
Muestreo y variabilidad
¿Cómo es posible que la media x̄ obtenida a partir de una muestra de unos pocos hogares de todos los del país, pueda ser una estimación precisa de µ?
Una segunda muestra aleatoria obtenida en el mismo momento estaría formada por hogares distintos y, sin duda, daría un valor distinto de x̄
Muestreo y variabilidad
Variabilidad muestral: el valor de un estadístico varía en un muestreo aleatorio repetido
¿Cuánto varía?
¿En qué rangos?
¿Qué tan probable es el rango de variación?
¿Es un rango aceptable en términos de investigación social?

Aleatoriedad y probabilidad
Llamamos a un fenómeno aleatorio si los resultados individuales son inciertos y, sin embargo, existe una distribución regular de los resultados después de un gran número de repeticiones.
Aleatoriedad y probabilidad
Llamamos a un fenómeno aleatorio si los resultados individuales son inciertos y, sin embargo, existe una distribución regular de los resultados después de un gran número de repeticiones.
La probabilidad de cualquier resultado de un fenómeno aleatorio es la proporción de veces que el resultado se da después de una larga serie de repeticiones
Azar y repetición
El comportamiento del azar es impredecible con pocas repeticiones pero presenta un comportamiento regular y predecible con muchas repeticiones.
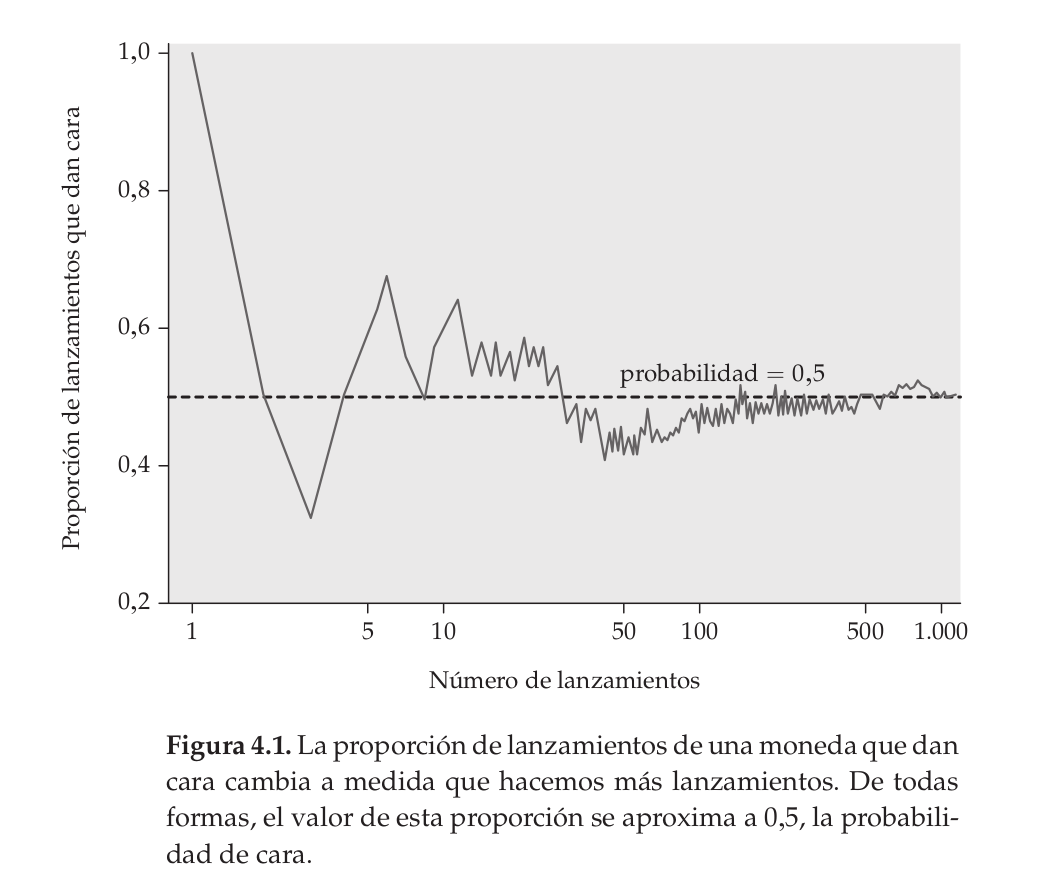
(Dato freak)
Cerca del año 1900, el estadístico inglés Karl Pearson lanzó al aire una moneda 24.000 veces. El resultado: 12.012 caras, una proporción de 0,5005.

Dados
Tenemos 1 dado, cuál es la probabilidad de que salga 3 al lanzarlo?
- Espacio muestral S= conjunto de todos los resultados posibles
S={1,2,3,4,5,6}S={1,2,3,4,5,6}
N del espacio muestral= 6 sucesos posibles
Probabilidad de que salga 3 al tirar el dado= 16=0.16616=0.166
Un modelo de probabilidad para un fenómeno aleatorio consiste en un espacio muestral S y una asignación de probabilidades P.
Un modelo de probabilidad para un fenómeno aleatorio consiste en un espacio muestral S y una asignación de probabilidades P.
El espacio muestral S es el conjunto de todos los resultados posibles de un fenómeno aleatorio.
Un modelo de probabilidad para un fenómeno aleatorio consiste en un espacio muestral S y una asignación de probabilidades P.
El espacio muestral S es el conjunto de todos los resultados posibles de un fenómeno aleatorio.
Un suceso es un conjunto de resultados. P asigna un número P(A) a un suceso A como su probabilidad.
Reglas modelo de probabilidad

Dados, probabilidades y áreas
Dados, probabilidades y áreas
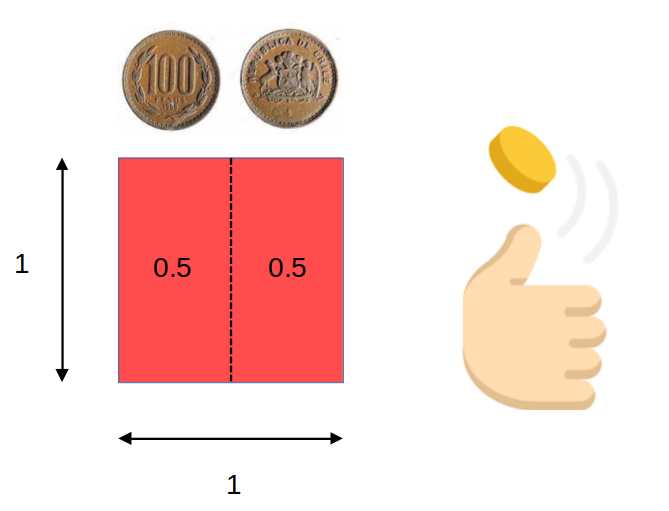
Dados, probabilidades y áreas
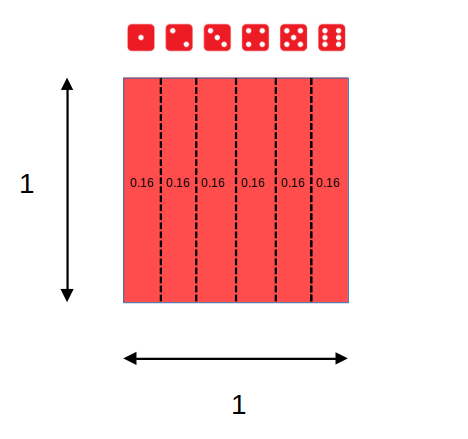
Dados, probabilidades y áreas
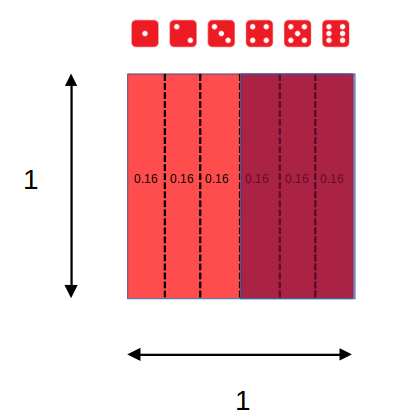
Eventos posibles (espacio muestral S) = 6 = (1,2,3,4,5,6)
P(x)≥4=P(4)+P(5)+P(6)=0.1¯6+0.1¯6+0.1¯6=0.5
Sucesos con distinta probabilidad
Ej: suma de 2 dados al azar repetidos
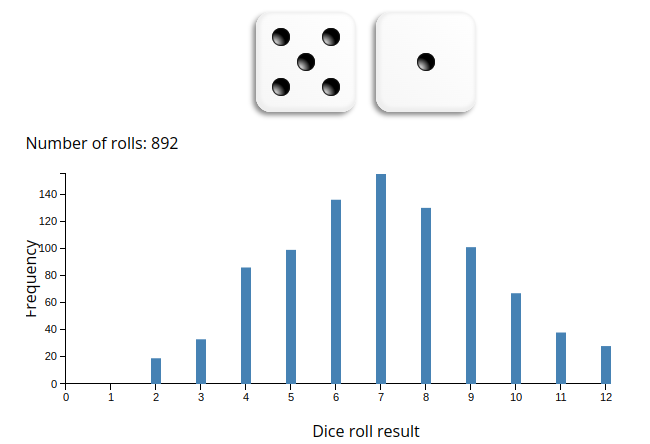
Distribución muestral del promedio
si extraemos repetidamente 2 dados, y obtenemos su promedio, el gráfico de frecuencias tenderá a una forma acampanada
esto ocurre simplemente porque la probabilidad de valores extremos (como promedio 1 o promedio 6) es mucho menor que la de obtener valores centrales
por lo tanto, podemos aproximarnos al promedio de la población mediante el promedio de los promedios de muchas muestras
ahora ...
¿Cómo estimar el promedio de los promedios con una sola muestra?
🤔
Próxima clase
-> Error estándar y distribución normal ... o cómo estimar el promedio de los promedios con una sola muestra
Y tarea:
# Generar todas las combinaciones posibles de dos dadosdado1 <- rep(1:6, each = 6)dado2 <- rep(1:6, times = 6)# Calcular la suma y el promedio para cada combinaciónsuma <- dado1 + dado2promedio <- suma / 2# Crear un data frame con los resultadosresultados <- data.frame(dado1, dado2, suma, promedio)# Mostrar el data frameprint(resultados)# Cargar la librería para gráficoslibrary(ggplot2)# Gráfico de frecuencias para la sumaggplot(resultados, aes(x = suma)) + geom_bar() + labs(title = "Gráfico de Frecuencias de la Suma", x = "Suma", y = "Frecuencia")# Gráfico de frecuencias para los promediosggplot(resultados, aes(x = promedio)) + geom_bar() + labs(title = "Gráfico de Frecuencias de los Promedios", x = "Promedio", y = "Frecuencia")Estadística Correlacional

