Pauta Prueba 2

Librerías y datos

# librerías
pacman::p_load(dplyr, sjPlot, sjmisc)

Pregunta 1 ¿En qué medida se relacionan los ingresos (en pesos) de las personas con sus niveles de autoritarismo?

1.1 Estime la correlación entre ambas variables utilizando R y genere un diagrama de dispersión (nube de puntos/scatterplot). Corte y pegue el código en el recuadro de abajo. (1p)

Forma A

cor.test(dataset1$ingresos, dataset1$autoritarismo, complete.obs = TRUE, method = "pearson")


    Pearson's product-moment correlation

data:  dataset1$ingresos and dataset1$autoritarismo
t = 39.93, df = 839, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7847979 0.8315542
sample estimates:
      cor 
0.8094554

sjPlot::plot_scatter(data = dataset1, x = ingresos, y = autoritarismo)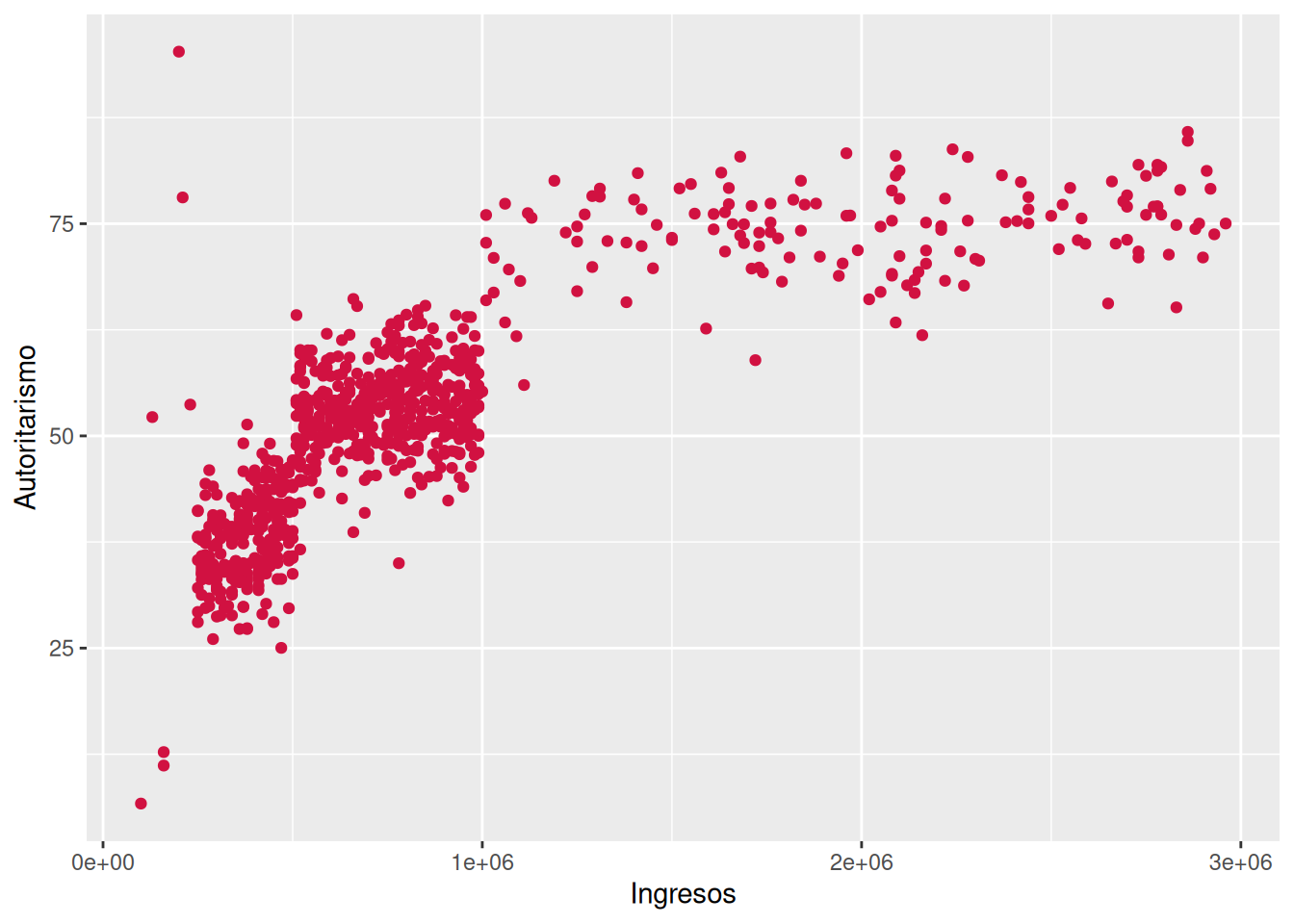

Forma B

cor.test(dataset2$ingresos, dataset2$autoritarismo, complete.obs = TRUE, method = "pearson")


    Pearson's product-moment correlation

data:  dataset2$ingresos and dataset2$autoritarismo
t = 1.215, df = 838, p-value = 0.2247
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.02578178  0.10926704
sample estimates:
       cor 
0.04193417

sjPlot::plot_scatter(data = dataset2, x = ingresos, y = autoritarismo)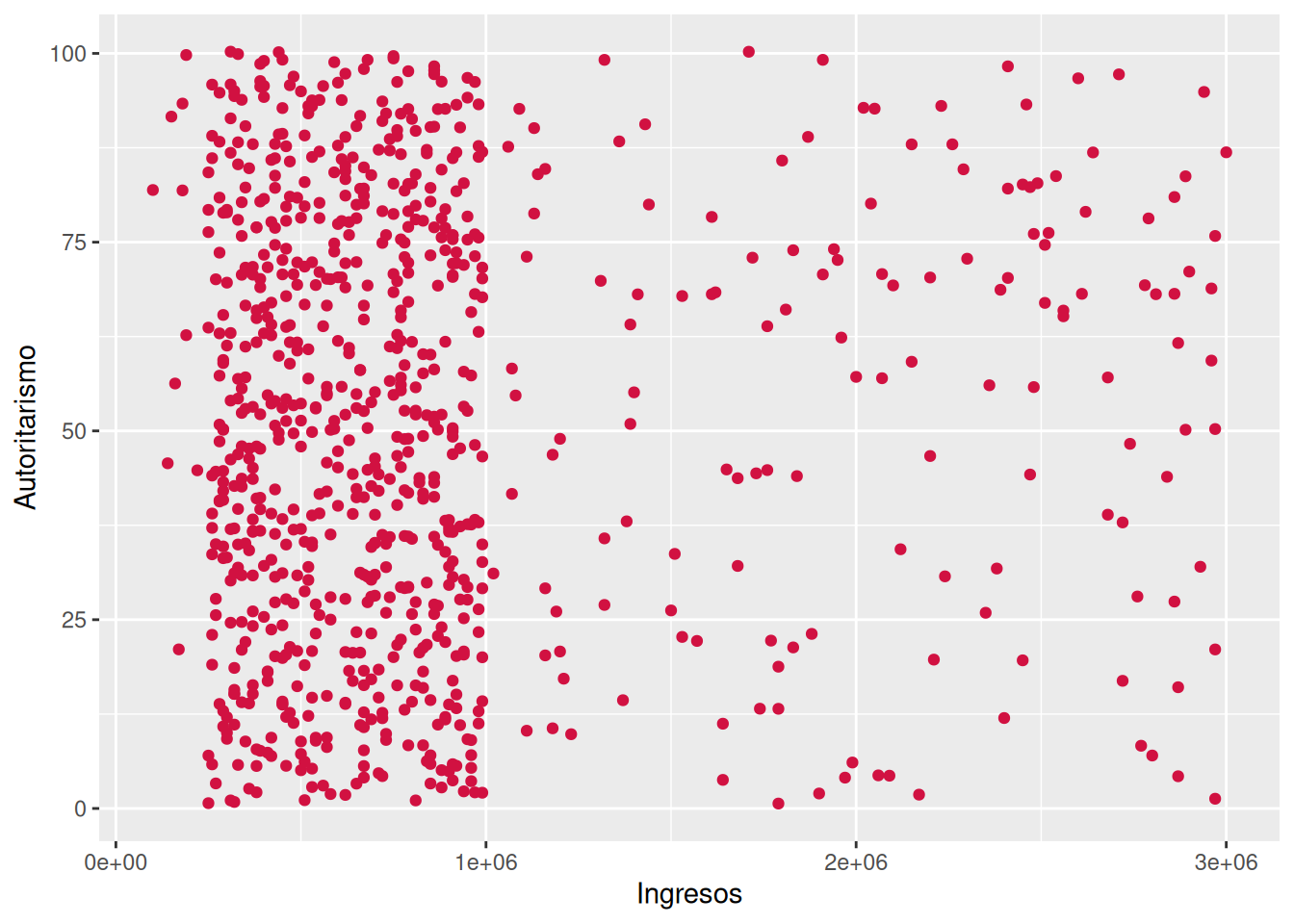

Forma C

cor.test(dataset3$ingresos, dataset3$autoritarismo, complete.obs = TRUE, method = "pearson")


    Pearson's product-moment correlation

data:  dataset3$ingresos and dataset3$autoritarismo
t = -0.88933, df = 842, p-value = 0.3741
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.09791381  0.03692461
sample estimates:
        cor 
-0.03063398

sjPlot::plot_scatter(data = dataset3, x = ingresos, y = autoritarismo)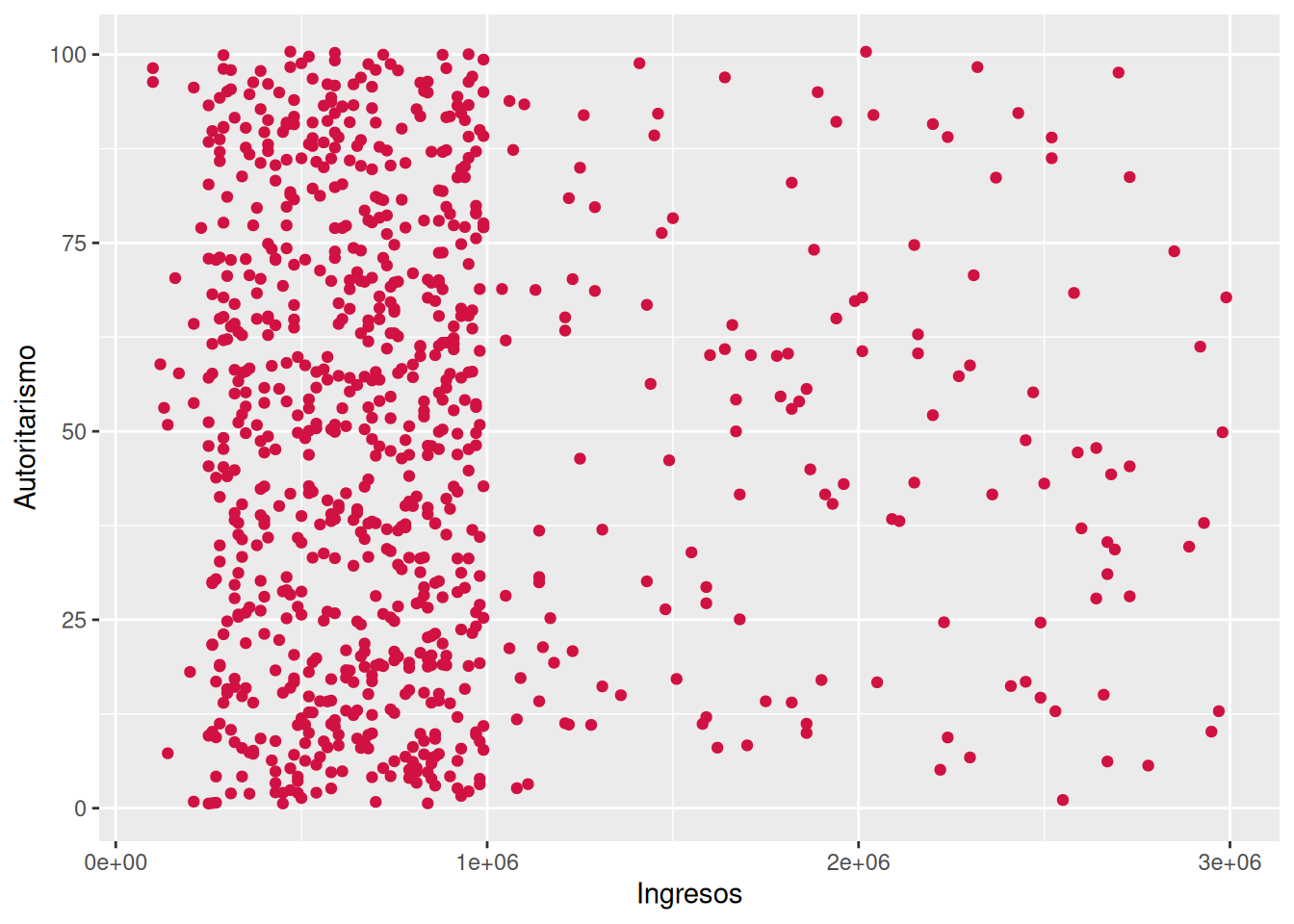

Forma D

cor.test(dataset4$ingresos, dataset4$autoritarismo, complete.obs = TRUE, method = "pearson")


    Pearson's product-moment correlation

data:  dataset4$ingresos and dataset4$autoritarismo
t = 37.907, df = 838, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7684251 0.8184034
sample estimates:
      cor 
0.7947577

sjPlot::plot_scatter(data = dataset4, x = ingresos, y = autoritarismo)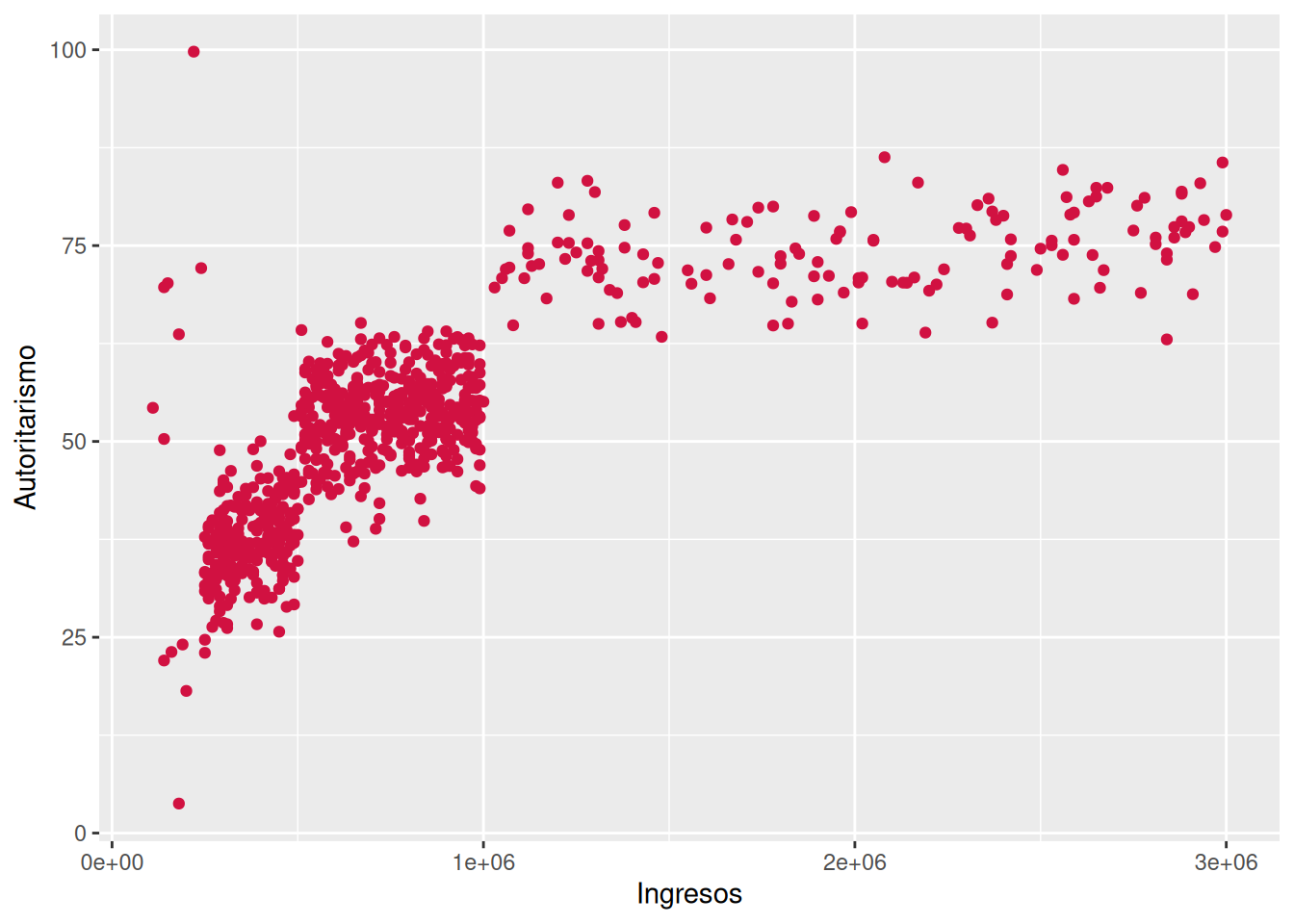

1.2 Justifique la elección del coeficiente de correlación seleccionado e interprete el resultado considerando inferencia estadística, magnitud y sentido del efecto. (3p)

Forma A: Se empleó el coeficiente de correlación de Pearson debido a la naturaleza de las variables, en tanto ingresos y autoritarismo corresponden a variables númericas de razón. El coeficiente da cuenta de una relacion positiva y grande, siguiendo los criterios de Cohen (1988) (\(r\) = 0.80). Es decir, a medida que aumentan los ingresos de las personas, también aumentan sus niveles de autoritarismo. La relación es estadísticamente significativa (\(p\) < 0.001), por ende es posible rechazar \(H_0\) sobre no asociación entre variables, entregando evidencia a favor de una relación entre ambas variables con un 99.9% de confianza.
Forma B: Se empleó el coeficiente de correlación de Pearson debido a la naturaleza de las variables, en tanto ingresos y autoritarismo corresponden a variables númericas de razón. El coeficiente da cuenta de una relacion positiva y muy pequeña, siguiendo los criterios de Cohen (1988) (\(r\) = 0.04). La relación no es estadísticamente significativa (\(p\) > 0.05), por ende no es posible rechazar \(H_0\) sobre no asociación entre variables al 95% de confianza.
Forma C: Se empleó el coeficiente de correlación de Pearson debido a la naturaleza de las variables, en tanto ingresos y autoritarismo corresponden a variables númericas de razón. El coeficiente da cuenta de una relacion negativa y muy pequeña, siguiendo los criterios de Cohen (1988) (\(r\) = -0.03). La relación no es estadísticamente significativa (\(p\) > 0.05), por ende no es posible rechazar \(H_0\) sobre no asociación entre variables al 95% de confianza.
Forma D: Se empleó el coeficiente de correlación de Pearson debido a la naturaleza de las variables, en tanto ingresos y autoritarismo corresponden a variables númericas de razón. El coeficiente da cuenta de una relacion positiva y grande, siguiendo los criterios de Cohen (1988) (\(r\) = 0.79). Es decir, a medida que aumentan los ingresos de las personas, también aumentan sus niveles de autoritarismo. La relación es estadísticamente significativa (p < 0.001), por ende es posible rechazar \(H_0\) sobre no asociación entre variables, entregando evidencia a favor de una relación entre ambas variables con un 99.9% de confianza.

NOTA: Si se utilizaba ingresos_rec y se señalaba que se escogía una correlación punto biserial, también se considera correcto.

Pregunta 2: ¿Cómo se relacionan el nivel educacional, autoritarismo y los ingresos?

2.1 Estime y reporte la matriz de correlaciones de las variables de nivel educacional, autoritarismo y los ingresos. Corte y pegue el código de R correspondiente (1p)

Forma A:

cormat <- dataset1 %>% 
  dplyr::select(educ_rec, autoritarismo, ingresos)
sjPlot::tab_corr(cormat, 
                 na.deletion = "pairwise", # espeficicamos tratamiento NA
                 triangle = "lower")

	Nivel educacinal recodificado (universitario o no)	Autoritarismo	Ingresos
Nivel educacinal recodificado (universitario o no)
Autoritarismo	-0.037
Ingresos	-0.030	0.809***
Computed correlation used pearson-method with pairwise-deletion.

sjPlot::tab_corr(cormat, 
                 na.deletion = "listwise", # espeficicamos tratamiento NA
                 triangle = "lower")

	Nivel educacinal recodificado (universitario o no)	Autoritarismo	Ingresos
Nivel educacinal recodificado (universitario o no)
Autoritarismo	-0.038
Ingresos	-0.027	0.809***
Computed correlation used pearson-method with listwise-deletion.

Forma B:

cormat <- dataset2 %>% 
  dplyr::select(educ_rec, autoritarismo, ingresos)
sjPlot::tab_corr(cormat, 
                 na.deletion = "pairwise", # espeficicamos tratamiento NA
                 triangle = "lower")

	Nivel educacinal recodificado (universitario o no)	Autoritarismo	Ingresos
Nivel educacinal recodificado (universitario o no)
Autoritarismo	0.059
Ingresos	0.837***	0.042
Computed correlation used pearson-method with pairwise-deletion.

sjPlot::tab_corr(cormat, 
                 na.deletion = "listwise", # espeficicamos tratamiento NA
                 triangle = "lower")

	Nivel educacinal recodificado (universitario o no)	Autoritarismo	Ingresos
Nivel educacinal recodificado (universitario o no)
Autoritarismo	0.078*
Ingresos	0.837***	0.042
Computed correlation used pearson-method with listwise-deletion.

Forma C:

cormat <- dataset3 %>% 
  dplyr::select(educ_rec, autoritarismo, ingresos)
sjPlot::tab_corr(cormat, 
                 na.deletion = "pairwise", # espeficicamos tratamiento NA
                 triangle = "lower")

	Nivel educacinal recodificado (universitario o no)	Autoritarismo	Ingresos
Nivel educacinal recodificado (universitario o no)
Autoritarismo	-0.029
Ingresos	0.041	-0.031
Computed correlation used pearson-method with pairwise-deletion.

sjPlot::tab_corr(cormat, 
                 na.deletion = "listwise", # espeficicamos tratamiento NA
                 triangle = "lower")

	Nivel educacinal recodificado (universitario o no)	Autoritarismo	Ingresos
Nivel educacinal recodificado (universitario o no)
Autoritarismo	-0.038
Ingresos	0.037	-0.031
Computed correlation used pearson-method with listwise-deletion.

Forma D:

cormat <- dataset4 %>% 
  dplyr::select(educ_rec, autoritarismo, ingresos)
sjPlot::tab_corr(cormat, 
                 na.deletion = "pairwise", # espeficicamos tratamiento NA
                 triangle = "lower")

	Nivel educacinal recodificado (universitario o no)	Autoritarismo	Ingresos
Nivel educacinal recodificado (universitario o no)
Autoritarismo	0.523***
Ingresos	0.831***	0.795***
Computed correlation used pearson-method with pairwise-deletion.

sjPlot::tab_corr(cormat, 
                 na.deletion = "listwise", # espeficicamos tratamiento NA
                 triangle = "lower")

	Nivel educacinal recodificado (universitario o no)	Autoritarismo	Ingresos
Nivel educacinal recodificado (universitario o no)
Autoritarismo	0.517***
Ingresos	0.830***	0.795***
Computed correlation used pearson-method with listwise-deletion.

2.2a ¿Qué correlaciones de la matriz son estadísticamente significativas? (1p)

Forma A:
- Pairwaise: La correlación de Pearson entre ingresos y autoritarismo es positiva, estadísticamente significativa (\(r\) = 0.809, \(p\) < 0.001) y fuerte según los criteriores de Cohen (1988).
- Listwise: La correlación de Pearson entre ingresos y autoritarismo es positiva, estadísticamente significativa (\(r\) = 0.809, \(p\) < 0.001) y fuerte según los criteriores de Cohen (1988).
Forma B:
- Pairwaise: La correlación de Pearson entre ingresos y nivel educacional es positiva, estadísticamente significativa (\(r\) = 0.837, \(p\) < 0.001) y fuerte según los criteriores de Cohen (1988).
- Listwise:
  1. La correlación de Pearson entre autoritarismo y nivel educacional es positiva, estadísticamente significativa (\(r\) = 0.078, \(p\) < 0.05) y débil según los criteriores de Cohen (1988).
  2. La correlación de Pearson entre ingresos y autoritarismo es positiva, estadísticamente significativa (\(r\) = 0.837, \(p\) < 0.05) y fuerte según los criteriores de Cohen (1988).
Forma C:
- Pairwaise: No hay asociaciones estadísticamente significativas (\(p\) < 0.05) entre las variables.
- Listwise: No hay asociaciones estadísticamente significativas (\(p\) < 0.05) entre las variables.
Forma D:
- Pairwaise:
  1. La correlación de Pearson entre autoritarismo y nivel educacional es positiva, estadísticamente significativa (\(r\) = 0.523, \(p\) < 0.001) y moderada según los criteriores de Cohen (1988).
  2. La correlación de Pearson entre ingresos y nivel educacional es positiva, estadísticamente significativa (\(r\) = 0.831, \(p\) < 0.001) y fuerte según los criteriores de Cohen (1988).
  3. La correlación de Pearson entre ingresos y autoritarismo es positiva, estadísticamente significativa (\(r\) = 0.795, \(p\) < 0.001) y fuerte según los criteriores de Cohen (1988).
- Listwise:
  1. La correlación de Pearson entre autoritarismo y nivel educacional es positiva, estadísticamente significativa (\(r\) = 0.517, \(p\) < 0.001) y moderada según los criteriores de Cohen (1988).
  2. La correlación de Pearson entre ingresos y nivel educacional es positiva, estadísticamente significativa (\(r\) = 0.830, \(p\) < 0.001) y fuerte según los criteriores de Cohen (1988).
  3. La correlación de Pearson entre ingresos y autoritarismo es positiva, estadísticamente significativa (\(r\) = 0.795, \(p\) < 0.001) y fuerte según los criteriores de Cohen (1988).

2.2b ¿Qué decisión tomó sobre los casos perdidos en el cálculo de la matriz? (1p)

Forma A:
- Pairwaise: Se optó por el método de eliminación de pares (pairwise) para el tratamiento de casos perdidos con el fin de mantener la mayor cantidad de casos a la hora de calcular estadísticos, especificamente respecto a la variable ingresos que tiene una alto porcentaje de valores perdidos (15%).
- Listwise: Se optó por el método de eliminación por lista (listwise) para el tratamiento de casos perdidos debido a que existe un alto porcentaje de valores perdidos en la variable ingresos (15%). El gran tamaño de la muestra (N=1.000) permite realizar este procedimiento.
Forma B:
- Pairwaise: Se optó por el método de eliminación de pares (pairwise) para el tratamiento de casos perdidos con el fin de mantener la mayor cantidad de casos a la hora de calcular estadísticos, especificamente respecto a la variable ingresos que tiene una alto porcentaje de valores perdidos (15%).
- Listwise: Se optó por el método de eliminación por lista (listwise) para el tratamiento de casos perdidos debido a que existe un alto porcentaje de valores perdidos en la variable ingresos (15%). El gran tamaño de la muestra (N=1.000) permite realizar este procedimiento.
Forma C:
- Pairwaise: Se optó por el método de eliminación de pares (pairwise) para el tratamiento de casos perdidos con el fin de mantener la mayor cantidad de casos a la hora de calcular estadísticos, especificamente respecto a la variable ingresos que tiene una alto porcentaje de valores perdidos (15%).
- Listwise: Se optó por el método de eliminación por lista (listwise) para el tratamiento de casos perdidos debido a que existe un alto porcentaje de valores perdidos en la variable ingresos (15%). El gran tamaño de la muestra (N=1.000) permite realizar este procedimiento.
Forma D:
- Pairwaise: Se optó por el método de eliminación de pares (pairwise) para el tratamiento de casos perdidos con el fin de mantener la mayor cantidad de casos a la hora de calcular estadísticos, especificamente respecto a la variable ingresos que tiene una alto porcentaje de valores perdidos (15%).
- Listwise: Se optó por el método de eliminación por lista (listwise) para el tratamiento de casos perdidos debido a que existe un alto porcentaje de valores perdidos en la variable ingresos (15%). El gran tamaño de la muestra (N=1.000) permite realizar este procedimiento.

2.2c ¿Cómo se denomina el tipo de correlación que se calcula entre nivel educacional e ingreso? (1p)

Forma A: La correlación entre la variable dummy nivel educacional (0=“No universitaria”; 1=“Universitaria o más”) y la variable continúa ingresos se denomina correlación punto biserial.
Forma B: La correlación entre la variable dummy nivel educacional (0=“No universitaria”; 1=“Universitaria o más”) y la variable continúa ingresos se denomina correlación punto biserial.
Forma C: La correlación entre la variable dummy nivel educacional (0=“No universitaria”; 1=“Universitaria o más”) y la variable continúa ingresos se denomina correlación punto biserial.
Forma D: La correlación entre la variable dummy nivel educacional (0=“No universitaria”; 1=“Universitaria o más”) y la variable continúa ingresos se denomina correlación punto biserial.

Pregunta 3: ¿Cómo se relaciona el nivel educacional con los ingresos?

3.1 Reporte tabla de contigencia y el cálculo de Chi2. Corte y pegue el código abajo. (1p)

Forma A:

pacman::p_load(sjPlot)
dataset1 %>%
  sjtab(educ_rec,
        ingresos_rec)

Nivel educacinal recodificado (universitario o no)	Ingresos recodificado			Total
Nivel educacinal recodificado (universitario o no)	Bajos ingresos	Medios ingresos	Altos ingresos	Total
No universitaria	162	262	103	527
Universitaria o más	92	180	51	323
Total	254	442	154	850
χ²=3.292 · df=2 · Cramer's V=0.062 · p=0.193

chisq.test(dataset1$educ_rec, dataset1$ingresos_rec) # adicional, ya que el Chi2 aparece en sjtab


    Pearson's Chi-squared test

data:  dataset1$educ_rec and dataset1$ingresos_rec
X-squared = 3.2921, df = 2, p-value = 0.1928

Forma B:

pacman::p_load(sjPlot)
dataset2 %>%
  sjtab(educ_rec,
        ingresos_rec)

Nivel educacinal recodificado (universitario o no)	Ingresos recodificado			Total
Nivel educacinal recodificado (universitario o no)	Bajos ingresos	Medios ingresos	Altos ingresos	Total
No universitaria	268	428	75	771
Universitaria o más	0	0	79	79
Total	268	428	154	850
χ²=393.623 · df=2 · Cramer's V=0.681 · p=0.000

chisq.test(dataset2$educ_rec, dataset2$ingresos_rec) # adicional, ya que el Chi2 aparece en sjtab


    Pearson's Chi-squared test

data:  dataset2$educ_rec and dataset2$ingresos_rec
X-squared = 393.62, df = 2, p-value < 2.2e-16

Forma C:

pacman::p_load(sjPlot)
dataset3 %>%
  sjtab(educ_rec,
        ingresos_rec)

Nivel educacinal recodificado (universitario o no)	Ingresos recodificado			Total
Nivel educacinal recodificado (universitario o no)	Bajos ingresos	Medios ingresos	Altos ingresos	Total
No universitaria	157	290	88	535
Universitaria o más	83	172	60	315
Total	240	462	148	850
χ²=1.405 · df=2 · Cramer's V=0.041 · p=0.495

chisq.test(dataset3$educ_rec, dataset3$ingresos_rec) # adicional, ya que el Chi2 aparece en sjtab


    Pearson's Chi-squared test

data:  dataset3$educ_rec and dataset3$ingresos_rec
X-squared = 1.4055, df = 2, p-value = 0.4952

Forma D:

pacman::p_load(sjPlot)
dataset4 %>%
  sjtab(educ_rec,
        ingresos_rec)

Nivel educacinal recodificado (universitario o no)	Ingresos recodificado			Total
Nivel educacinal recodificado (universitario o no)	Bajos ingresos	Medios ingresos	Altos ingresos	Total
No universitaria	269	437	73	779
Universitaria o más	0	0	71	71
Total	269	437	144	850
χ²=379.824 · df=2 · Cramer's V=0.668 · p=0.000

chisq.test(dataset4$educ_rec, dataset4$ingresos_rec) # adicional, ya que el Chi2 aparece en sjtab


    Pearson's Chi-squared test

data:  dataset4$educ_rec and dataset4$ingresos_rec
X-squared = 379.82, df = 2, p-value < 2.2e-16

3.2 Interprete el Chi2 en términos de inferencia y magnitud del efecto. (3p)

Forma A: χ2=3.292 · df=2 · Cramer’s V=0.062 · p=0.193 Chi cuadrado no es estadísticamente significativo (p > 0.05), tamaño de efecto pequeño/débil según la V de Cramer
Forma B: χ2=393.623 · df=2 · Cramer’s V=0.681 · p=0.000 Chi cuadrado estadísticamente significativo (p < 0.001), tamaño de efecto grande/fuerte según la V de Cramer
Forma C: χ2=1.405 · df=2 · Cramer’s V=0.041 · p=0.495 Chi cuadrado no es estadísticamente significativo (p > 0.05), tamaño de efecto pequeño/débil según la V de Cramer
Forma D: χ2=379.824 · df=2 · Cramer’s V=0.668 · p=0.000 Chi cuadrado estadísticamente significativo (p < 0.001), tamaño de efecto grande/fuerte según la V de Cramer